Cheguei ate aqui e parei ñ resolvie brother...




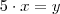
 , então para termos o total de bombons temos que somar o número de bombons das 4 crianças, logo:
, então para termos o total de bombons temos que somar o número de bombons das 4 crianças, logo: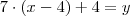
 é o número de crianças que irá receber os 7 bombons, isto é, o total de crianças, x, menos as 4 que receberão 1 bombom cada. Mas
é o número de crianças que irá receber os 7 bombons, isto é, o total de crianças, x, menos as 4 que receberão 1 bombom cada. Mas  só me diz quantos bombons teremos quando dermos os 7 bombons para as crianças, para termos o total de bombons da caixa temos que somar os 4 bombons das crianças que só receberão 1 bombom cada, isto é, 4 crianças, então a equação fica daquele jeito.
só me diz quantos bombons teremos quando dermos os 7 bombons para as crianças, para termos o total de bombons da caixa temos que somar os 4 bombons das crianças que só receberão 1 bombom cada, isto é, 4 crianças, então a equação fica daquele jeito.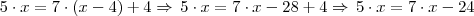




Voltar para Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.