Boa tarde, Antônio!
Há um erro na verificação que fiz (1º
post).
Observei o seguinte: a lei de formação da soma é dada por
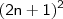
; ora, o primeiro termo é determinado substituindo "n" por zero, veja:
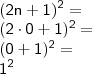
E, se substituíres "n" por zero na expressão do lado direito da igualdade, perceberás que é verdadeira.
Por conseguinte, tomei n = 1. Daí,
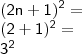
Uma vez que, não faz mui sentido ter n = 0, aplicamos a seguinte estratégia: passe o termo

para o outro lado da igualdade. Desse modo, poderemos ter
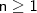
.
Tomemos como hipótese que a igualdade seja verdadeira para
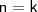
, com
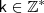
; então,
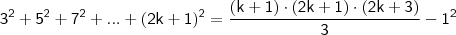
Isto posto, sabemos do Princípio da Indução Finita (1ª forma) que a igualdade será válida se

. Ou seja,

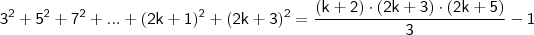
É a tese de indução!!
Agora, devemos prová-la. Segue, da hipótese que:
![\\ \mathsf{\underbrace{\mathsf{3^2 + 5^2 + 7^2 + ... + (2k + 1)^2}}_{hip\acute{o}tese} + (2k + 3)^2 =} \\\\\\ \mathsf{\left [ \frac{(k + 1)(2k + 1)(2k + 3)}{3} - 1 \right ] + (2k + 3)^2 =} \\\\\\ \mathsf{\frac{(k + 1)(2k + 1)(2k + 3)}{3} + (2k + 3)^2 - 1 =} \\\\\\ \mathsf{(2k + 3) \cdot \left [ \frac{(k + 1)(2k + 1)}{3} + (2k + 3) \right ] - 1 =} \\ \mathsf{\underbrace{\mathsf{3^2 + 5^2 + 7^2 + ... + (2k + 1)^2}}_{hip\acute{o}tese} + (2k + 3)^2 =} \\\\\\ \mathsf{\left [ \frac{(k + 1)(2k + 1)(2k + 3)}{3} - 1 \right ] + (2k + 3)^2 =} \\\\\\ \mathsf{\frac{(k + 1)(2k + 1)(2k + 3)}{3} + (2k + 3)^2 - 1 =} \\\\\\ \mathsf{(2k + 3) \cdot \left [ \frac{(k + 1)(2k + 1)}{3} + (2k + 3) \right ] - 1 =}](/latexrender/pictures/ab882dba143c02eb52a0861658d4adeb.png)

![\\ \mathsf{(2k + 3) \cdot \frac{(k + 2) \cdot \left [ 2k + 5 \right ]}{3} - 1 =} \\\\\\ \mathsf{\frac{(2k + 3) \cdot (k + 2) \cdot \left (2k + 5) \right ]}{3} - 1} \\ \mathsf{(2k + 3) \cdot \frac{(k + 2) \cdot \left [ 2k + 5 \right ]}{3} - 1 =} \\\\\\ \mathsf{\frac{(2k + 3) \cdot (k + 2) \cdot \left (2k + 5) \right ]}{3} - 1}](/latexrender/pictures/5b5f7bca792fc6651fc3ba24b812e104.png)
Ufa! Repare que isto (acima) corresponde à tese!
Como queríamos demonstrar!


 ; ou seja,
; ou seja, 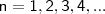 .
. - elemento mínimo. Vejamos:
- elemento mínimo. Vejamos: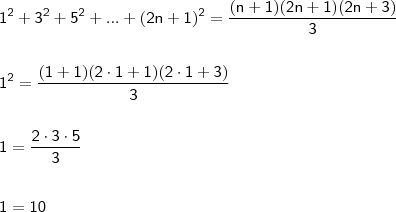

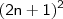 ; ora, o primeiro termo é determinado substituindo "n" por zero, veja:
; ora, o primeiro termo é determinado substituindo "n" por zero, veja: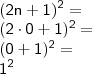
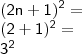
 para o outro lado da igualdade. Desse modo, poderemos ter
para o outro lado da igualdade. Desse modo, poderemos ter 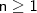 .
.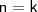 , com
, com 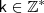 ; então,
; então,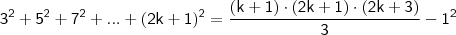
 . Ou seja,
. Ou seja,
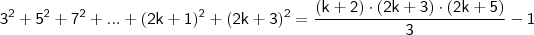
![\\ \mathsf{\underbrace{\mathsf{3^2 + 5^2 + 7^2 + ... + (2k + 1)^2}}_{hip\acute{o}tese} + (2k + 3)^2 =} \\\\\\ \mathsf{\left [ \frac{(k + 1)(2k + 1)(2k + 3)}{3} - 1 \right ] + (2k + 3)^2 =} \\\\\\ \mathsf{\frac{(k + 1)(2k + 1)(2k + 3)}{3} + (2k + 3)^2 - 1 =} \\\\\\ \mathsf{(2k + 3) \cdot \left [ \frac{(k + 1)(2k + 1)}{3} + (2k + 3) \right ] - 1 =} \\ \mathsf{\underbrace{\mathsf{3^2 + 5^2 + 7^2 + ... + (2k + 1)^2}}_{hip\acute{o}tese} + (2k + 3)^2 =} \\\\\\ \mathsf{\left [ \frac{(k + 1)(2k + 1)(2k + 3)}{3} - 1 \right ] + (2k + 3)^2 =} \\\\\\ \mathsf{\frac{(k + 1)(2k + 1)(2k + 3)}{3} + (2k + 3)^2 - 1 =} \\\\\\ \mathsf{(2k + 3) \cdot \left [ \frac{(k + 1)(2k + 1)}{3} + (2k + 3) \right ] - 1 =}](/latexrender/pictures/ab882dba143c02eb52a0861658d4adeb.png)

![\\ \mathsf{(2k + 3) \cdot \frac{(k + 2) \cdot \left [ 2k + 5 \right ]}{3} - 1 =} \\\\\\ \mathsf{\frac{(2k + 3) \cdot (k + 2) \cdot \left (2k + 5) \right ]}{3} - 1} \\ \mathsf{(2k + 3) \cdot \frac{(k + 2) \cdot \left [ 2k + 5 \right ]}{3} - 1 =} \\\\\\ \mathsf{\frac{(2k + 3) \cdot (k + 2) \cdot \left (2k + 5) \right ]}{3} - 1}](/latexrender/pictures/5b5f7bca792fc6651fc3ba24b812e104.png)
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.