Estou resolvendo a lista de sequencias e series e estou com problema em uma devida questão, que diz o seguinte:
"Mostre que a função f determinada pelo n-ésimo termo da série verifica as hipóteses do teste da integral. Além disso, use o teste da integral para determinar se a serie converge ou diverge."
Então, eu não sei bem como testar essas hipoteses, e acredito que seja isso o problema, porque eu fiz o processo todo da integral e no fim deu infinito, que faria a serie divergir, porem utilizando um aplicativo o mesmo diz que a serie converge, então não sei bem o que estou errado, se alguem poder me ajudar, a questão e a seguinte:
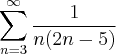
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)