 por HenriqueOrlan » Sáb Nov 21, 2015 11:28
por HenriqueOrlan » Sáb Nov 21, 2015 11:28
Olá, estou com uma dúvida em relação à séries.
Tenho a seguinte série:

E quero usar algum dos testes disponíveis para saber se ela converge ou diverge. Já que k vai para infinito, o termo dominante do numerador seria

, e o termo dominante do denominador seria
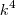
. Então posso simplificar a expressão para
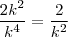
para fim de teste de convergência?
Obrigado.
-
HenriqueOrlan
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Nov 21, 2015 11:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por adauto martins » Qua Nov 25, 2015 16:31
por adauto martins » Qua Nov 25, 2015 16:31
sim,é isso mesmo...numa serie em q. o termo geral é uma divisao de polinomios ou funçoes quaisquer,toma-se a divisao de suas ordens,p/criterio de convergia...logo tal serie converge...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Séries] Dúvida sobre divergência de série
por leticia_08 » Sáb Abr 19, 2014 20:12
- 7 Respostas
- 4397 Exibições
- Última mensagem por Russman

Dom Abr 20, 2014 13:42
Sequências
-
- Séries
por Guilherme Carvalho » Seg Set 17, 2012 22:50
- 5 Respostas
- 3439 Exibições
- Última mensagem por Guilherme Carvalho

Ter Set 18, 2012 16:24
Sequências
-
- Séries
por manuoliveira » Sex Mai 23, 2014 21:07
- 2 Respostas
- 2184 Exibições
- Última mensagem por Man Utd

Ter Mai 27, 2014 15:10
Sequências
-
- Sequencias e Séries
por Neperiano » Dom Set 26, 2010 19:28
- 1 Respostas
- 2255 Exibições
- Última mensagem por Marcampucio

Dom Set 26, 2010 21:36
Cálculo: Limites, Derivadas e Integrais
-
- Séries de pagamentos!
por Clara19 » Qua Abr 06, 2011 00:47
- 1 Respostas
- 2279 Exibições
- Última mensagem por Rogerio Murcila

Qua Mai 11, 2011 13:56
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 , e o termo dominante do denominador seria
, e o termo dominante do denominador seria 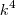 . Então posso simplificar a expressão para
. Então posso simplificar a expressão para 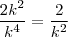 para fim de teste de convergência?
para fim de teste de convergência?



 .
.



