[Sequencias] Calculo do limite da sequencia

por **Larissa28** » Qua Ago 05, 2015 01:09

Calcule o limite, se existir, (se não, justifique) da sequencia de termo geral

$an = \sqrt[n]{{2}^{1+3n}}$

por **nakagumahissao** » Qua Ago 05, 2015 16:32

${a}_{n} = \sqrt[n]{{2}^{1+3n}}$

${a}_{2} = \sqrt[2]{{2}^{7}} = \sqrt[2]{{2}^{6} \times 2} = 2^{3} \sqrt[2]{2} = 8\sqrt[2]{2}$

${a}_{3} = \sqrt[3]{{2}^{10}} = \sqrt[3]{{2}^{9} \times 2} = 2^{3} \sqrt[3]{2} = 8\sqrt[3]{2}$

${a}_{4} = \sqrt[4]{{2}^{13}} = \sqrt[4]{{2}^{12} \times 2} = 2^{3} \sqrt[4]{2} = 8\sqrt[4]{2}$

e assim sucessivamente. Para n = n, teremos:

${a}_{n} = 8\sqrt[n]{2}$

Assim:

${a}_{n} = \sqrt[n]{{2}^{1+3n}} = 8\sqrt[n]{2}$

Vejamos alguns valores para:

Seja ${b}_{n} = \sqrt[n]{2}$

$n = 2 \Rightarrow {b}_{2} = \sqrt[2]{2} = 1,4142$
$n = 3 \Rightarrow {b}_{3} = \sqrt[3]{2} = 1,2599$
$n = 4 \Rightarrow {b}_{4} = \sqrt[4]{2} = 1,1892$
$n = 5 \Rightarrow {b}_{5} = \sqrt[5]{2} = 1,1486$

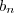Ou seja, ${b}_{n}$ é decrescente e portanto ${a}_{n}$ também é decrescente.

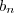Sendo decrescente e positiva, suspeitamos agora que a sequêcia seja limitada inferiormente, pois ${b}_{n}$ parece convergir para 1 e ${a}_{n}$ parece estar convergindo para 8. Então:

$\lim_{n \rightarrow \infty } 8\sqrt[n]{2} = \lim_{n \rightarrow \infty } 8 \cdot 2^{\frac{1}{n}} = \lim_{n \rightarrow \infty } 8 * \lim_{n \rightarrow \infty } {2}^{\frac{1}{n}} = 8 \times 1 = 8$

Pois, à medida que n "tende" ao infinito, n se torna um número "grande" e 1 dividido por esse número cada vez "maior", vai se aproximando de zero e 2 elevado à zero vai se tornar 1 e 1 vezes 8 dá 8.