Para a area eu calcularia a area dos semi-cilindros e depois o da intersecção deles
a area na intersecção poderia ser claculada dividindo a intersecção em quatro partes iguais , então calculando uma das partes teria a area total.
pegando como base o cilindro sobre o eixo x temos que sua equação é dada por

sendo que isso é valido para para y<x e -y>-x
podemos dividir este setor em infinitos arcos de comprimento ds para cada valor de x
assim calculando a area teriamos
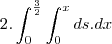
mais temos que ds é

então a integral dupla da area fica

calculando a derivada e substituindo

fazendo uma troca de variaveis na ordem de integração

integrando com relação a x
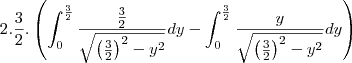
a primeira integrla se calcula por substituição tirgonometrica ja a segunda por substituição de variavel calculando voce vai ter uma area das quatros interesecções, multiplicando por 4 tera a area da região central, fora dessa região pode se utilizar a formula do calculo da area do cilindro, somando as areas tem a area total da figura.



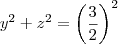






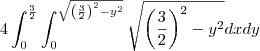
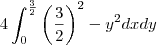
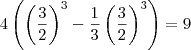



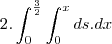




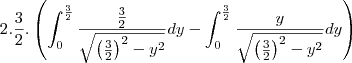






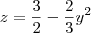




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
