preciso de ajuda na resoluçao dos exercicios, não estou pedindo p/ que façam o trabalho pra mim, pois o importante é eu aprender a fazer, tentei fazer uns em casa que foram :2) a,b,c,d,e,f,g,h,
3)a,b
o exercicio numero 1) a,b eu nao consegui fazer
a letra i, do numero 2, tbm nao consegui fazer
o exercicio numero 4, nao consegui fazer nenhum, pois nao sei usar o geogebra, nao precisa me mostrar o grafico somente conjunto, imgem e dominio.
se alguem puder me ajudar, eu agradeço.
1) se f(x)=-x²+1/x+2
a) f(-1) b) f(x+1) c) f(x/3) d) f (1/1+t)
2) determine o conjunto, imagem e dominio: i) f(x)=e elevado a 2x
4) determinar conjunto, imgem e dominio
infelizmente nao consegui editar os exercicios,pois nao sei domonar esse programa do editor de formulas. vou ter q enviar como anexo a lista.
é minha primeira vez aqui, mas com o tempo au aprendo.obrigada,


 .
. ; b)
; b) 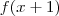 .
.  . Calcule g(a) , g(x+1) , g(2) .
. Calcule g(a) , g(x+1) , g(2) .  .
. .
.
 .
.  .
. . Veja
. Veja 

 .
.



