 por mih123 » Seg Set 03, 2012 22:41
por mih123 » Seg Set 03, 2012 22:41
Boa Noite! Alguém pode me ajudar a resolver essa questão?
![\lim_{x\to3}\frac{{\left|x-3\right|}^{2}+26\left|x+3 \right|-26\sqrt[2]{\sqrt[2]{3x}+33}}{4-2\sqrt[3]{\frac{x^2+15x-6}{x+3}}} \lim_{x\to3}\frac{{\left|x-3\right|}^{2}+26\left|x+3 \right|-26\sqrt[2]{\sqrt[2]{3x}+33}}{4-2\sqrt[3]{\frac{x^2+15x-6}{x+3}}}](/latexrender/pictures/17bef8d8f0a8499cea46779a9daa08ab.png)
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por mih123 » Ter Set 04, 2012 23:47
por mih123 » Ter Set 04, 2012 23:47
A parte do denominador eu entendi,mas não consigo fazer o numerador.Não esta dando certo ;/
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qua Set 05, 2012 00:54
por e8group » Qua Set 05, 2012 00:54
Boa noite .
Note que ,
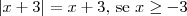

.
Mas como
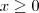
.Isto é , se o numerador é uma função , seu domínio estar limitado aos números reais positivos .
Sendo assim ,
![|x-3|^2 + 26[ |x+3| - ( (3x)^{1/2} +33) ^{1/2} ] = (x-3)^2 + 26[x+3 - (\sqrt{3}x^{1/2}+33)^{1/2}] |x-3|^2 + 26[ |x+3| - ( (3x)^{1/2} +33) ^{1/2} ] = (x-3)^2 + 26[x+3 - (\sqrt{3}x^{1/2}+33)^{1/2}]](/latexrender/pictures/5cfd28bbc987a5dd0c418332ae576e1e.png)
.
logo ,
![\left((x-3)^2 + 26[x+3 - (\sqrt{3}x^{1/2}+33)^{1/2}] \right)' = \left((x-3)^2 + 26[x+3 - (\sqrt{3}x^{1/2}+33)^{1/2}] \right)' =](/latexrender/pictures/f1f3493e05337cf8ebb419b1658f4c4f.png)
![= \frac{\mathrm{d} (x-3)^2}{\mathrm{d} (x-3)}\cdot \frac{\mathrm{d} (x-3)}{\mathrm{d} x} + 26 \left[\frac{\mathrm{d}( x+3)}{\mathrm{d} x} - \frac{\mathrm{d} (\sqrt{3}x^{1/2}+33)^{1/2}}{\mathrm{d} (\sqrt{3}x^{1/2}+33)}\cdot \sqrt{3}\cdot
\frac{\mathrm{d} x^{1/2}}{\mathrm{d} x} \right ] = = \frac{\mathrm{d} (x-3)^2}{\mathrm{d} (x-3)}\cdot \frac{\mathrm{d} (x-3)}{\mathrm{d} x} + 26 \left[\frac{\mathrm{d}( x+3)}{\mathrm{d} x} - \frac{\mathrm{d} (\sqrt{3}x^{1/2}+33)^{1/2}}{\mathrm{d} (\sqrt{3}x^{1/2}+33)}\cdot \sqrt{3}\cdot
\frac{\mathrm{d} x^{1/2}}{\mathrm{d} x} \right ] =](/latexrender/pictures/07504e249327068d081b96cb81147ac8.png)
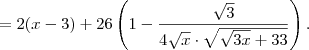
.
Como você conseguiu derivar o denominador ,poderá calcular o limite .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mih123 » Qua Set 12, 2012 11:19
por mih123 » Qua Set 12, 2012 11:19
Muitoo Obrigada!

-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo de Limite] Resolução de um limite
por julianocoutinho » Seg Mai 13, 2013 01:47
- 3 Respostas
- 3315 Exibições
- Última mensagem por Man Utd

Qua Mai 15, 2013 22:26
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de exercício
 por Flavia Araujo » Qui Mai 21, 2009 14:38
por Flavia Araujo » Qui Mai 21, 2009 14:38
- 28 Respostas
- 35701 Exibições
- Última mensagem por Neperiano

Ter Fev 23, 2010 13:50
Progressões
-
- resolução de exercício
 por jose henrique » Sex Nov 12, 2010 21:20
por jose henrique » Sex Nov 12, 2010 21:20
- 2 Respostas
- 2425 Exibições
- Última mensagem por MarceloFantini

Sex Nov 12, 2010 22:58
Trigonometria
-
- Resolução de Exercicio Urgente
por Mimizinha » Qua Mar 19, 2008 18:13
- 7 Respostas
- 18242 Exibições
- Última mensagem por Mimizinha

Qui Mar 20, 2008 12:58
Sistemas de Equações
-
- Ajuda com resolução do exercicio
por Mimizinha » Ter Abr 01, 2008 10:27
- 3 Respostas
- 5753 Exibições
- Última mensagem por admin

Ter Abr 01, 2008 23:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\to3}\frac{{\left|x-3\right|}^{2}+26\left|x+3 \right|-26\sqrt[2]{\sqrt[2]{3x}+33}}{4-2\sqrt[3]{\frac{x^2+15x-6}{x+3}}} \lim_{x\to3}\frac{{\left|x-3\right|}^{2}+26\left|x+3 \right|-26\sqrt[2]{\sqrt[2]{3x}+33}}{4-2\sqrt[3]{\frac{x^2+15x-6}{x+3}}}](/latexrender/pictures/17bef8d8f0a8499cea46779a9daa08ab.png)


![\lim_{x\to3}\frac{{\left|x-3\right|}^{2}+26\left|x+3 \right|-26\sqrt[2]{\sqrt[2]{3x}+33}}{4-2\sqrt[3]{\frac{x^2+15x-6}{x+3}}} \lim_{x\to3}\frac{{\left|x-3\right|}^{2}+26\left|x+3 \right|-26\sqrt[2]{\sqrt[2]{3x}+33}}{4-2\sqrt[3]{\frac{x^2+15x-6}{x+3}}}](/latexrender/pictures/17bef8d8f0a8499cea46779a9daa08ab.png)



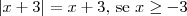
 .
. 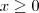 .Isto é , se o numerador é uma função , seu domínio estar limitado aos números reais positivos .
.Isto é , se o numerador é uma função , seu domínio estar limitado aos números reais positivos . ![|x-3|^2 + 26[ |x+3| - ( (3x)^{1/2} +33) ^{1/2} ] = (x-3)^2 + 26[x+3 - (\sqrt{3}x^{1/2}+33)^{1/2}] |x-3|^2 + 26[ |x+3| - ( (3x)^{1/2} +33) ^{1/2} ] = (x-3)^2 + 26[x+3 - (\sqrt{3}x^{1/2}+33)^{1/2}]](/latexrender/pictures/5cfd28bbc987a5dd0c418332ae576e1e.png) .
. ![\left((x-3)^2 + 26[x+3 - (\sqrt{3}x^{1/2}+33)^{1/2}] \right)' = \left((x-3)^2 + 26[x+3 - (\sqrt{3}x^{1/2}+33)^{1/2}] \right)' =](/latexrender/pictures/f1f3493e05337cf8ebb419b1658f4c4f.png)
![= \frac{\mathrm{d} (x-3)^2}{\mathrm{d} (x-3)}\cdot \frac{\mathrm{d} (x-3)}{\mathrm{d} x} + 26 \left[\frac{\mathrm{d}( x+3)}{\mathrm{d} x} - \frac{\mathrm{d} (\sqrt{3}x^{1/2}+33)^{1/2}}{\mathrm{d} (\sqrt{3}x^{1/2}+33)}\cdot \sqrt{3}\cdot
\frac{\mathrm{d} x^{1/2}}{\mathrm{d} x} \right ] = = \frac{\mathrm{d} (x-3)^2}{\mathrm{d} (x-3)}\cdot \frac{\mathrm{d} (x-3)}{\mathrm{d} x} + 26 \left[\frac{\mathrm{d}( x+3)}{\mathrm{d} x} - \frac{\mathrm{d} (\sqrt{3}x^{1/2}+33)^{1/2}}{\mathrm{d} (\sqrt{3}x^{1/2}+33)}\cdot \sqrt{3}\cdot
\frac{\mathrm{d} x^{1/2}}{\mathrm{d} x} \right ] =](/latexrender/pictures/07504e249327068d081b96cb81147ac8.png)
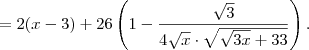 .
.


