Volume do solido

por **ivoski** » Ter Ago 14, 2012 17:38

Preciso de uma ajuda nesta questao, abraços a todos

Use uma integral dupla para calcular o volume do sólido delimitado pelas superfícies y=0, y= 1-x² , x²+z=1 e z=0

por **LuizAquino** » Qui Ago 16, 2012 21:26

ivoski escreveu:Preciso de uma ajuda nesta questao, abraços a todos

Use uma integral dupla para calcular o volume do sólido delimitado pelas superfícies y=0, y= 1-x² , x²+z=1 e z=0

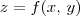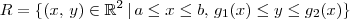Você precisa determinar uma função $z = f(x,\, y)$ (tal que $f(x,y) \geq 0$ ) e uma região no plano xy dada por $R = \{(x,\,y)\in\mathbb{R}^2 \,|\, a \leq x \leq b,\, g_1(x)\leq y \leq g_2(x) \}$ . Nesse caso, o volume desejado será: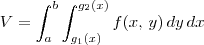

$\displaystyle V = \int_a^b \int_{g_1(x)}^{g_2(x)} f(x,\,y)\,dy \,dx$

De x^2 + z = 1

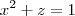, você pode escrever z = 1 - x^2

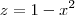. Note que você pode enxergar z como uma função de x e y (mesmo que y não apareça em sua expressão). Ou seja, você pode escrever que 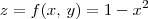$z = f(x,\,y) = 1 - x^2$ . Além disso, note que $f(x,\,y) \geq 0$ , pois o sólido deve estar delimitado inferiormente pelo plano z = 0 (ou seja, o plano xy).

Considerando agora que o sólido também está delimitado pelo plano y = 0 (ou seja, o plano xz) e pela superfície y = 1 - x^2

, podemos obter a região no plano xy dada por $R = \{(x,\,y)\in\mathbb{R}^2 \,|\, -1 \leq x \leq 1,\, 0\leq y \leq 1 - x^2\}$ .

Usando todas as informações, o volume procurado será dado por:

$\displaystyle V = \int_{-1}^1 \int_{0}^{1 - x^2} 1 - x^2\,dy \,dx$

Agora tente concluir o exercício.

por **ivoski** » Qui Ago 16, 2012 22:52

Obrigado Luiz Aquino... consegui terminar esta questao com sua ajuda
se poder me ajuda nas outras duas que postei
obrigado... abraços

Volume do solido

Volume do solido

Volume do solido

Re: Volume do solido

Re: Volume do solido

Quem está online