Tenho também uma dúvida acerca de raízes.
Tenho uma função x^6+3x^5 = -1
Pedem-me, mostre que a equação tem uma raiz em ]-1, 0 [
Ora, o que eu costumo fazer é derivar, o que me dá 6x^5+ 15x^4
Como não consigo calcular assim os zeros, simplifiquei : x^3(x^2 + 15x) = 0 o que me dá um zero em x=-15, o que supostamente me ensinaram foi que se a derivada não tiver zeros existe apenas um zero na função.
Assim a derivada tem zeros.
Alguém me pode ajudar a resolver isto ?


 deve mudar de sinal entre
deve mudar de sinal entre 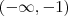 e
e 
 e outro de
e outro de 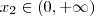 e mostrar que
e mostrar que 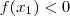 e
e  .
.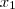 eu escolho, por exemplo
eu escolho, por exemplo  . Assim,
. Assim,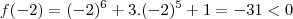 .
.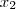 eu escolho, por exemplo
eu escolho, por exemplo  . Assim,
. Assim,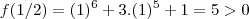 .
. .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)