 por arturvr » Sex Mai 25, 2012 23:14
por arturvr » Sex Mai 25, 2012 23:14
Boa noite pessoal, blz? Alguém poderia me ajudar nessa integral:
?(1/R^2) * ((1-r/R)^( 1/7)) rdr
variando de 0 a R.
Abraços e obrigado!
-
arturvr
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Mai 25, 2012 23:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Petróleo
- Andamento: cursando
 por LuizAquino » Sáb Mai 26, 2012 08:01
por LuizAquino » Sáb Mai 26, 2012 08:01
arturvr escreveu:Boa noite pessoal, blz? Alguém poderia me ajudar nessa integral:
?(1/R^2) * ((1-r/R)^( 1/7)) rdr
variando de 0 a R.
Você deseja calcular:
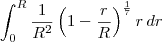
Para estudar uma integral, eu gostaria de lhe dar uma dica. Você pode usar um programa para isso! Por exemplo, o
SAGE, o Mathematica, o Maple, etc.
Alguns desses programas são disponibilizados também na forma de uma página na internet. É o caso do
SAGE Notebook e do Mathematica. Por exemplo, siga os passos abaixo para conferir a resolução da integral indefinida associada a esse problema.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (1/R^2)((1-r/R)^( 1/7))r dr
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução.
Depois que você determinou o resultado da integral indefinida, fica fácil calcular a integral definida.
Você também pode conferir o resultado final da integral definida substituindo o código do passo 2 por:
- Código: Selecionar todos
integrate (1/R^2)((1-r/R)^( 1/7))r dr, r=0..R
ObservaçãoEu gostaria de recomendar que você leia o tópico abaixo para saber como digitar de forma adequada todas as notações matemáticas aqui no fórum.
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com integral
por Marcossiva » Ter Jul 09, 2013 17:29
- 3 Respostas
- 1630 Exibições
- Última mensagem por Marcossiva

Sex Jul 12, 2013 12:12
Cálculo: Limites, Derivadas e Integrais
-
- Integral ajuda
por Barcosta » Sáb Mar 29, 2014 19:10
- 0 Respostas
- 922 Exibições
- Última mensagem por Barcosta

Sáb Mar 29, 2014 19:10
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda numa integral...
por macburn » Ter Nov 02, 2010 15:51
- 17 Respostas
- 11720 Exibições
- Última mensagem por MarceloFantini

Qui Nov 04, 2010 17:20
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com integral envolvendo tgx e sen^2x
por kryzay » Qua Mar 07, 2012 09:02
- 4 Respostas
- 2555 Exibições
- Última mensagem por kryzay

Qua Mar 07, 2012 15:34
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda em Integral Iterada
 por Cleyson007 » Qua Abr 18, 2012 16:50
por Cleyson007 » Qua Abr 18, 2012 16:50
- 1 Respostas
- 833 Exibições
- Última mensagem por DanielFerreira

Qua Abr 18, 2012 21:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



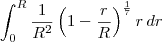



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.