 por Russman » Qua Mai 23, 2012 18:49
por Russman » Qua Mai 23, 2012 18:49
Eu gostaria de saber se vocês concordam ou não com o seguinte:
Eu quero calcular a integral de uma função do tipo
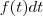
, ou seja, uma função multiplicada por um diferencial.
Se
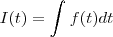
, então
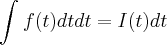
.
Posso pensar assim? Tenho motivos para achar que sim! Mas...
Obrigado.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Mai 24, 2012 10:41
por Russman » Qui Mai 24, 2012 10:41
UP!
Ninguem? ;(
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por fraol » Sáb Mai 26, 2012 00:40
por fraol » Sáb Mai 26, 2012 00:40
Interessante!
Meu palpite ... é que é possível, pensar assim.
Embora não tenha estudado isso diretamente, me parece mais uma questão de notação pois acabaríamos em uma integral iterada, não?
Aliás, a qual assunto ou aplicação você está relacionando isso?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por nietzsche » Sáb Mai 26, 2012 17:14
por nietzsche » Sáb Mai 26, 2012 17:14
Quando você escreve
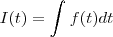
, está querendo dizer o que com o lado direito?
Normalmente, a notação
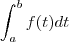
indica que sua variável de integração

está variando entre

e

.
Então se você multiplica por um diferencial dt,
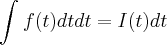
você está multiplicando pelo que? O diferencial dt indica o que? Quais motivos que te levam a pensar que pode multplicar por dt? Eu creio que não pode.
Existem várias formas de se abordar integral:
http://en.wikipedia.org/wiki/Integral
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Mai 27, 2012 15:36
por MarceloFantini » Dom Mai 27, 2012 15:36
Não tenho domínio suficiente sobre o assunto, mas praticamente certeza que esta "operação" não existe. Um diferencial é um elemento do espaço dos tensores alternantes com a operação produto exterior. Isto significa que é anticomutativo, isto é,

(como o produto vetorial). Quando são iguais, isto é nulo. Mas, mesmo para fazer isto, é necessário que você possa definir o produto exterior. A integral é um número, não se "aplica" um diferencial dentro dela.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Russman » Dom Mai 27, 2012 19:01
por Russman » Dom Mai 27, 2012 19:01
Obrigado, pessoal! ;D
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- diferencial e integral
por edilaine33 » Seg Dez 02, 2013 20:08
- 1 Respostas
- 1386 Exibições
- Última mensagem por Bravim

Seg Dez 02, 2013 20:13
Cálculo: Limites, Derivadas e Integrais
-
- diferencial e integral
 por edilaine33 » Seg Dez 02, 2013 20:20
por edilaine33 » Seg Dez 02, 2013 20:20
- 0 Respostas
- 782 Exibições
- Última mensagem por edilaine33

Seg Dez 02, 2013 20:20
Cálculo: Limites, Derivadas e Integrais
-
- cálculo diferencial e integral
por Neperiano » Qua Out 08, 2008 22:20
- 4 Respostas
- 7058 Exibições
- Última mensagem por admin

Ter Out 14, 2008 16:41
Cálculo: Limites, Derivadas e Integrais
-
- calculo integral e diferencial
 por edilainemorais » Qui Fev 20, 2014 18:15
por edilainemorais » Qui Fev 20, 2014 18:15
- 0 Respostas
- 1953 Exibições
- Última mensagem por edilainemorais

Qui Fev 20, 2014 18:15
Cálculo: Limites, Derivadas e Integrais
-
- cálculo diferencial e integral II
por Luiz vicente » Seg Mar 06, 2017 13:30
- 0 Respostas
- 6609 Exibições
- Última mensagem por Luiz vicente

Seg Mar 06, 2017 13:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
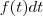 , ou seja, uma função multiplicada por um diferencial.
, ou seja, uma função multiplicada por um diferencial.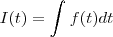 , então
, então 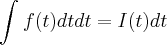 .
.
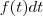 , ou seja, uma função multiplicada por um diferencial.
, ou seja, uma função multiplicada por um diferencial.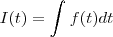 , então
, então 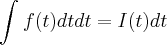 .
.


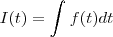 , está querendo dizer o que com o lado direito?
, está querendo dizer o que com o lado direito? 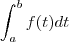 indica que sua variável de integração
indica que sua variável de integração  está variando entre
está variando entre  e
e  .
. 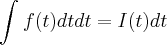 você está multiplicando pelo que? O diferencial dt indica o que? Quais motivos que te levam a pensar que pode multplicar por dt? Eu creio que não pode.
você está multiplicando pelo que? O diferencial dt indica o que? Quais motivos que te levam a pensar que pode multplicar por dt? Eu creio que não pode.
 (como o produto vetorial). Quando são iguais, isto é nulo. Mas, mesmo para fazer isto, é necessário que você possa definir o produto exterior. A integral é um número, não se "aplica" um diferencial dentro dela.
(como o produto vetorial). Quando são iguais, isto é nulo. Mas, mesmo para fazer isto, é necessário que você possa definir o produto exterior. A integral é um número, não se "aplica" um diferencial dentro dela.



 .
.



