por Catalao » Qua Mai 09, 2012 19:51
por Catalao » Qua Mai 09, 2012 19:51
Galera hj a minha prof passou uma derivada na sala e ninguem conseguiu fazer... nem ela auhhauha...
Gostaria de saber se tem como alguem me ajudar...
f(x)= x^x
p=1
Ela quer saber f'(1)
Ai fica :
f'(1)=lim x->1 de x^x - 1/ x -1 = lim x->1 e^x.ln(x) -1/ x-1
Aí paramos por aqui...
Nós seguimos o livro do guidorizzi e no livro ele passou uma "dica"
lim h->0 e^h - 1/h = lim h->0 u/ln(u+1) = lim u->0 1/(1/u . ln(u+1) = lim u->0 1/ln((u+1)^1/u) = lim u->0 1/ln(e) = 1/1 = 1
lembrando que e^h-1=u
Tipo nesse limite ele cai no limite fundamental... talvez o limite de cima de f'(1) tbm tenha que cair... mas como?
Se alguem puder me ajudar eu agradeço!!
Abraços.
-
Catalao
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Mai 09, 2012 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por joaofonseca » Qua Mai 09, 2012 20:28
por joaofonseca » Qua Mai 09, 2012 20:28
E se você escreve-se as expressões matematicas utilizando o Latex?
Só com muita boa vontade é que alguém vai pegar na sua questão e resolve-la!!!!!!!!!
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Catalao » Sex Mai 11, 2012 19:28
por Catalao » Sex Mai 11, 2012 19:28
Desculpa... n sei mexer no Latex ainda mas vou tenttar escrever:
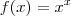
p=1
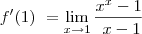
=
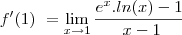
O limite que o Guidorizzi dá a dica é o seguinte:
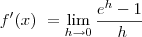
=
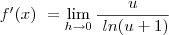
=
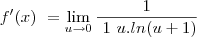
=
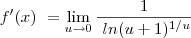
=
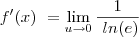
=
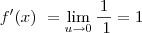
Bom pessoal tentei ai fazer com o Latex mas é a minha primeira vez usando-o... detalhe: na terceira passagem do guidorizzi é 1 SOBRE 1Sobre u.ln(u+1)... n sabia com fazer esse... mas espero que isso tenha melhorado a minha pergunta... se alguem puder me ajudar por favor ja ficarei grata!!!
Abraços.
-
Catalao
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Mai 09, 2012 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Seg Mai 14, 2012 14:55
por LuizAquino » Seg Mai 14, 2012 14:55
Catalao escreveu: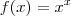
p=1
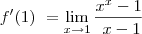
=
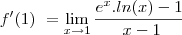
O limite que o Guidorizzi dá a dica é o seguinte:
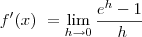
=
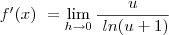
=
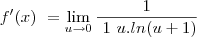
=
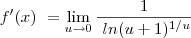
=
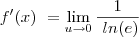
=
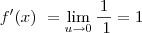
Bom pessoal tentei ai fazer com o Latex mas é a minha primeira vez usando-o... detalhe: na terceira passagem do guidorizzi é 1 SOBRE 1Sobre u.ln(u+1)... n sabia com fazer esse... mas espero que isso tenha melhorado a minha pergunta... se alguem puder me ajudar por favor ja ficarei grata!
Esse exercício está no livro de Guidorizzi? Qual é a edição que você está usando? Além disso, em que página, seção e capítulo está esse exercício?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Não consigo resolver essa questão com derivada
por Cristiano Tavares » Sáb Jun 18, 2011 12:18
- 2 Respostas
- 1827 Exibições
- Última mensagem por Cristiano Tavares

Sáb Jun 18, 2011 15:07
Cálculo: Limites, Derivadas e Integrais
-
- P.A nao consigo resolver essa p.a.
por Dalila » Sex Nov 14, 2008 16:58
- 2 Respostas
- 3130 Exibições
- Última mensagem por admin

Sex Nov 14, 2008 17:29
Progressões
-
- Não consigo resolver essa integral
por Cristiano Tavares » Qua Mai 11, 2011 22:16
- 2 Respostas
- 2072 Exibições
- Última mensagem por Cristiano Tavares

Qua Mai 11, 2011 23:59
Cálculo: Limites, Derivadas e Integrais
-
- Quádricas não consigo desenvolver essa questão
por berg_nascimento » Qui Jun 30, 2016 14:58
- 0 Respostas
- 1457 Exibições
- Última mensagem por berg_nascimento

Qui Jun 30, 2016 14:58
Geometria Analítica
-
- [INDUÇÃO | DIVISIBILIDADE] ñ consigo iniciar essa questão
por juliohenriquelima14 » Sáb Dez 13, 2014 19:03
- 3 Respostas
- 3133 Exibições
- Última mensagem por juliohenriquelima14

Sáb Dez 13, 2014 23:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



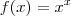
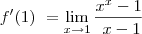 =
= 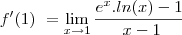
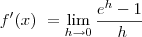 =
= 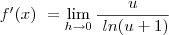 =
= 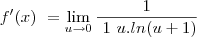 =
= 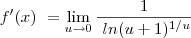 =
= 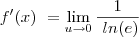 =
=