 por Cleyson007 » Qui Mai 03, 2012 09:38
por Cleyson007 » Qui Mai 03, 2012 09:38
Bom dia a todos!
Calcule a integral iterada
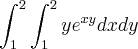
Consegui desenvolver até aqui:
![\int_{1}^{2}y\left [\frac{e^{xy}}{y} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}\left [ e^{xy} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}(e^{2y}-e^{y})\,dy \int_{1}^{2}y\left [\frac{e^{xy}}{y} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}\left [ e^{xy} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}(e^{2y}-e^{y})\,dy](/latexrender/pictures/b2ca695ddd2765b5997c74650ec548a1.png)
Preciso de ajuda para prosseguir.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Qui Mai 03, 2012 10:17
por LuizAquino » Qui Mai 03, 2012 10:17
Cleyson007 escreveu:Calcule a integral iterada
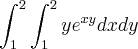
Consegui desenvolver até aqui:
![\int_{1}^{2}y\left [\frac{e^{xy}}{y} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}\left [ e^{xy} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}(e^{2y}-e^{y})\,dy \int_{1}^{2}y\left [\frac{e^{xy}}{y} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}\left [ e^{xy} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}(e^{2y}-e^{y})\,dy](/latexrender/pictures/b2ca695ddd2765b5997c74650ec548a1.png)
Preciso de ajuda para prosseguir.
Lembre-se que:


-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Cleyson007 » Qui Mai 03, 2012 11:12
por Cleyson007 » Qui Mai 03, 2012 11:12
Bom dia Luiz Aquino!
Luiz, essa dica que você me passou é regra? Sempre vai ser assim?
![\int_{1}^{2}(e^{2y}-e^{y})\,dy\Rightarrow \left [ \frac{1}{2}e^{2y}+c-(e^y+c) \right ]_{1}^{2} \int_{1}^{2}(e^{2y}-e^{y})\,dy\Rightarrow \left [ \frac{1}{2}e^{2y}+c-(e^y+c) \right ]_{1}^{2}](/latexrender/pictures/f79cd7aa461bd1751060cad5933eb576.png)
![\left [ \frac{e^{2y}}{2}\,-\,e^y \right ]_{1}^{2}\Rightarrow \left ( \frac{e^{4}}{2}\,-\,e^2 \right )-\left ( \frac{e^{2}}{2}\,-\,e \right ) \left [ \frac{e^{2y}}{2}\,-\,e^y \right ]_{1}^{2}\Rightarrow \left ( \frac{e^{4}}{2}\,-\,e^2 \right )-\left ( \frac{e^{2}}{2}\,-\,e \right )](/latexrender/pictures/ccdb8d09dbc804faec941c283e9e7cd6.png)

Está correto?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Qui Mai 03, 2012 11:23
por LuizAquino » Qui Mai 03, 2012 11:23
Cleyson007 escreveu:Luiz, essa dica que você me passou é regra? Sempre vai ser assim?
Provavelmente você já sabe que a derivada da função

é dada por
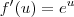
.
Considere então a integral:
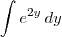
O que acontece se você resolver essa integral através da substituição u = 2y?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Cleyson007 » Qui Mai 03, 2012 11:55
por Cleyson007 » Qui Mai 03, 2012 11:55
Bom dia Luiz Aquino!
Considerando a integral
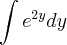
.
No meu ponto de vista, se eu resolvê-la fazendo uso da substituição
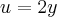
, terei:

Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Qui Mai 03, 2012 12:01
por LuizAquino » Qui Mai 03, 2012 12:01
Cleyson007 escreveu:Considerando a integral
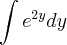
.
No meu ponto de vista, se eu resolvê-la fazendo uso da substituição
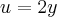
, terei:

O resultado é esse. Mas você não escreveu adequadamente a subsituição.
Considerando a substituição u = 2y, temos que du = 2dy. Desse modo, temos que:
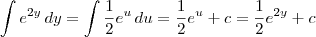
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguém sabe como prosseguir?
por Cleyson007 » Qua Mai 09, 2012 12:21
- 1 Respostas
- 1300 Exibições
- Última mensagem por MarceloFantini

Qua Mai 09, 2012 21:40
Álgebra Elementar
-
- Duvida , não consigo prosseguir com o calculo"Help"
por klysman » Ter Mai 01, 2012 20:38
- 5 Respostas
- 2517 Exibições
- Última mensagem por DanielFerreira

Qua Mai 02, 2012 23:10
Geometria Analítica
-
- Oi como vai...
por Fiel8 » Qua Jul 01, 2009 16:59
- 1 Respostas
- 4339 Exibições
- Última mensagem por Cleyson007

Qua Jul 01, 2009 18:11
Sistemas de Equações
-
- Sen a = 4/5 cos b = 2/3 como a < 0 e b < ?/2
por Parole » Sex Set 30, 2011 18:34
- 0 Respostas
- 3246 Exibições
- Última mensagem por Parole

Sex Set 30, 2011 18:34
Trigonometria
-
- Sen a = 4/5 cos b = 2/3 como a < 0 e b < ?/2
por Parole » Sex Set 30, 2011 18:36
- 0 Respostas
- 2782 Exibições
- Última mensagem por Parole

Sex Set 30, 2011 18:36
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
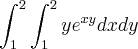
![\int_{1}^{2}y\left [\frac{e^{xy}}{y} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}\left [ e^{xy} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}(e^{2y}-e^{y})\,dy \int_{1}^{2}y\left [\frac{e^{xy}}{y} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}\left [ e^{xy} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}(e^{2y}-e^{y})\,dy](/latexrender/pictures/b2ca695ddd2765b5997c74650ec548a1.png)

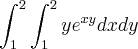
![\int_{1}^{2}y\left [\frac{e^{xy}}{y} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}\left [ e^{xy} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}(e^{2y}-e^{y})\,dy \int_{1}^{2}y\left [\frac{e^{xy}}{y} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}\left [ e^{xy} \right ]_{1}^{2}dy\Rightarrow \int_{1}^{2}(e^{2y}-e^{y})\,dy](/latexrender/pictures/b2ca695ddd2765b5997c74650ec548a1.png)




![\int_{1}^{2}(e^{2y}-e^{y})\,dy\Rightarrow \left [ \frac{1}{2}e^{2y}+c-(e^y+c) \right ]_{1}^{2} \int_{1}^{2}(e^{2y}-e^{y})\,dy\Rightarrow \left [ \frac{1}{2}e^{2y}+c-(e^y+c) \right ]_{1}^{2}](/latexrender/pictures/f79cd7aa461bd1751060cad5933eb576.png)
![\left [ \frac{e^{2y}}{2}\,-\,e^y \right ]_{1}^{2}\Rightarrow \left ( \frac{e^{4}}{2}\,-\,e^2 \right )-\left ( \frac{e^{2}}{2}\,-\,e \right ) \left [ \frac{e^{2y}}{2}\,-\,e^y \right ]_{1}^{2}\Rightarrow \left ( \frac{e^{4}}{2}\,-\,e^2 \right )-\left ( \frac{e^{2}}{2}\,-\,e \right )](/latexrender/pictures/ccdb8d09dbc804faec941c283e9e7cd6.png)


 é dada por
é dada por 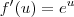 .
.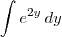

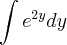 .
.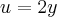 , terei:
, terei:

.
, terei:
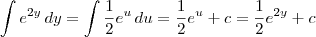



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.