Calcule a integral iterada
 e esboce sua região de integração R.
e esboce sua região de integração R.Se alguém puder me ajudar, ficarei grato.
Aguardo retorno.

 e esboce sua região de integração R.
e esboce sua região de integração R.
Cleyson007 escreveu:Bom dia a todos!
Calcule a integral iteradae esboce sua região de integração R.

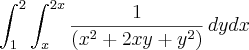


Cleyson007 escreveu:Apresentando minha resolução:
Primeiramente, gostaria de saber se até aqui está correto.
![\int_x^{2x} \frac{1}{(x+y)^2}\, dy = \int_{2x}^{3x} \frac{1}{u^2}\, du = \left[-\frac{1}{u}\right]_{2x}^{3x} = -\frac{1}{3x} + \frac{1}{2x} \int_x^{2x} \frac{1}{(x+y)^2}\, dy = \int_{2x}^{3x} \frac{1}{u^2}\, du = \left[-\frac{1}{u}\right]_{2x}^{3x} = -\frac{1}{3x} + \frac{1}{2x}](/latexrender/pictures/8e7922710d06bd7ad7ce91cdad4b84cf.png)


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)