 por Henrique Bueno » Ter Abr 17, 2012 18:35
por Henrique Bueno » Ter Abr 17, 2012 18:35
O limite fornecido foi
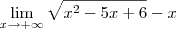
multipliquei em cima e em baixo por

obtendo:
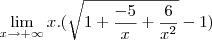
obtendo:
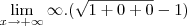
que dá 0. porém, o gabarito diz -5/2.. Onde foi que eu errei? hehe
obrigado
-
Henrique Bueno
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Mar 02, 2011 19:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Ter Abr 17, 2012 22:35
por fraol » Ter Abr 17, 2012 22:35
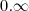
é uma indeterminação.
Uma melhor racionalização seria multiplicar por
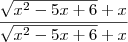
. Assim você obterá um produto notável no numerador. Depois é só aplicar propriedades de limite para chegar ao resultado correto.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida na minha resolução
por zenildo » Sex Abr 15, 2016 15:10
- 1 Respostas
- 2502 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 23, 2016 15:56
Inequações
-
- Está certa minha resolução???
por Valmel » Qui Dez 06, 2012 00:48
- 1 Respostas
- 1901 Exibições
- Última mensagem por Valmel

Qui Dez 06, 2012 00:51
Aritmética
-
- [Integral Definida] Está certa minha resolução?
por Fabio Wanderley » Seg Out 22, 2012 23:37
- 2 Respostas
- 2033 Exibições
- Última mensagem por Fabio Wanderley

Ter Out 23, 2012 00:45
Cálculo: Limites, Derivadas e Integrais
-
- Esta minha resolucao está correta?
por SsEstevesS » Dom Nov 27, 2011 10:29
- 0 Respostas
- 2968 Exibições
- Última mensagem por SsEstevesS

Dom Nov 27, 2011 10:29
Geometria Plana
-
- [Cálculo de Limite] Resolução de um limite
por julianocoutinho » Seg Mai 13, 2013 01:47
- 3 Respostas
- 3325 Exibições
- Última mensagem por Man Utd

Qua Mai 15, 2013 22:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
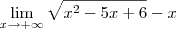
 obtendo:
obtendo: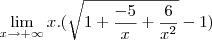
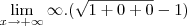

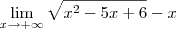
 obtendo:
obtendo: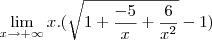
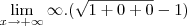

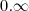 é uma indeterminação.
é uma indeterminação.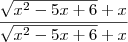 . Assim você obterá um produto notável no numerador. Depois é só aplicar propriedades de limite para chegar ao resultado correto.
. Assim você obterá um produto notável no numerador. Depois é só aplicar propriedades de limite para chegar ao resultado correto.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.