-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478598 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534018 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 497565 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 712058 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2132715 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
Como solucionar esse tipo de limite com raiz??
![\lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x} \lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x}](/latexrender/pictures/c75cecf4ecdb298b02d38e536f78ea66.png)
É a minha primeira vez no fórum, estou com uma certa dificuldade para montar essa fórmula. No exemplo acima, é uma raiz dentro da outra .. No caso, os três primeiros 'x', depois vem diminuindo essa última raiz. Deu pra entender??
Estou enviando anexo uma foto que tirei do meu caderno com a fórmula correta. rs
Estou estudando Limites no período da faculdade, e deparei com esse exemplo na minha lista de exercicios.
Não sei como saio disso .. rs
- Anexos
-
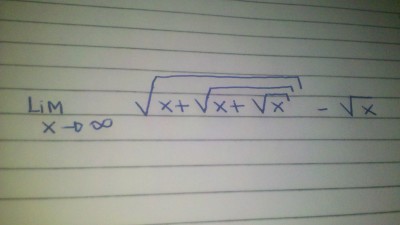
- Como resolver este tipo de Limite ?
-
natyncb
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 12, 2012 00:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 12:33
por LuizAquino » Qui Abr 12, 2012 12:33
natyncb escreveu:Como solucionar esse tipo de limite com raiz??
![\lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x} \lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x}](/latexrender/pictures/c75cecf4ecdb298b02d38e536f78ea66.png)
É a minha primeira vez no fórum, estou com uma certa dificuldade para montar essa fórmula. No exemplo acima, é uma raiz dentro da outra .. No caso, os três primeiros 'x', depois vem diminuindo essa última raiz. Deu pra entender??
Estou enviando anexo uma foto que tirei do meu caderno com a fórmula correta. rs
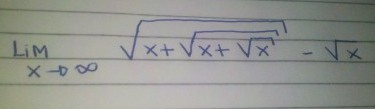
- figura.jpg (7.63 KiB) Exibido 12127 vezes
Estou estudando Limites no período da faculdade, e deparei com esse exemplo na minha lista de exercicios.
Não sei como saio disso .. rs
O limite desejado é:
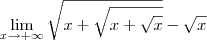
Para escrever esse limite aqui no fórum, use o código:
- Código: Selecionar todos
[tex]\lim_{x\to +\infty} \sqrt{x + \sqrt{x + \sqrt{x}}} - \sqrt{x}[/tex]
Para começar a resolver, multiplique e divida a expressão dentro do limite por
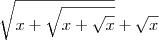
. Nesse caso, temos que:
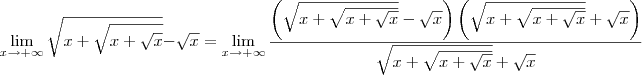
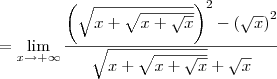

Agora divida o numerador e o denominador por

. Nesse caso, temos que:
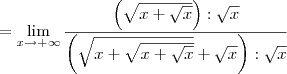
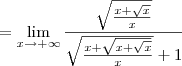

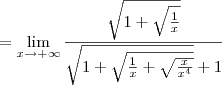
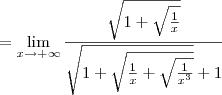
Agora tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por natyncb » Qui Abr 12, 2012 12:45
por natyncb » Qui Abr 12, 2012 12:45
Meio caminho andando, agora vou tentar resolver aqui ..
Muito obrigada pela ajuda !
-
natyncb
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 12, 2012 00:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por natyncb » Qui Abr 12, 2012 15:26
por natyncb » Qui Abr 12, 2012 15:26
Fiquei quebrando a cabeça aqui tentando resolver o restante da questão.
Consegui encontrar 1 como resposta.
Será que está certo, ou devo refazer tudo ?? hahaaa
-
natyncb
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 12, 2012 00:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 17:48
por LuizAquino » Qui Abr 12, 2012 17:48
natyncb escreveu:Fiquei quebrando a cabeça aqui tentando resolver o restante da questão.
Consegui encontrar 1 como resposta.
Será que está certo, ou devo refazer tudo ??
A reposta não é 1.
Lembre-se que:
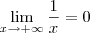
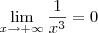
Desse modo, temos que:
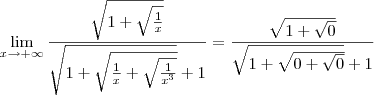

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por doleand » Ter Ago 21, 2012 23:43
por doleand » Ter Ago 21, 2012 23:43
não consegui entender o q foi feito ao certo... se puder me esclarecer...
-
doleand
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 21, 2012 22:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia de produção
- Andamento: cursando
 por LuizAquino » Qua Ago 22, 2012 07:41
por LuizAquino » Qua Ago 22, 2012 07:41
doleand escreveu:não consegui entender o q foi feito ao certo... se puder me esclarecer...
Exatamente que parte você não entendeu?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por doleand » Qua Ago 22, 2012 16:11
por doleand » Qua Ago 22, 2012 16:11
Agora divida o numerador e o denominador por raiz de x, (desta parte em diante)
-
doleand
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 21, 2012 22:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia de produção
- Andamento: cursando
 por LuizAquino » Qui Ago 23, 2012 19:09
por LuizAquino » Qui Ago 23, 2012 19:09
doleand escreveu:Agora divida o numerador e o denominador por raiz de x, (desta parte em diante)
Pois bem, temos o seguinte limite:
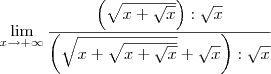
Vamos desenvolver o numerador. Note que escrever
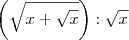
é o mesmo que escrever

. Mas lembrando de propriedades de radiciação, sabemos que

. Desse modo, temos que:

Por outro lado, sabemos que

. Desse modo, podemos escrever que:
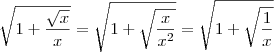
Em resumo, temos que
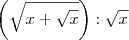
é equivalente a

Agora tente usar ideias semelhantes para desenvolver o denominador.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por doleand » Sex Ago 24, 2012 00:32
por doleand » Sex Ago 24, 2012 00:32
muito obrigada vc esclareceu algumas pendencias de anos atrás,dúvidas q eu nem sabia que tinha...valeu mesmo, brigadão!!!

-
doleand
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 21, 2012 22:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia de produção
- Andamento: cursando
 por LuizAquino » Sex Ago 24, 2012 07:50
por LuizAquino » Sex Ago 24, 2012 07:50
doleand escreveu:muito obrigada vc esclareceu algumas pendencias de anos atrás,dúvidas q eu nem sabia que tinha...valeu mesmo, brigadão!!!

Seria interessante que você fizesse uma revisão dos conteúdos de Matemática dos níveis fundamental e médio. Com certeza isso ajudará no seu aprendizado de Cálculo.
Por exemplo, assista as videoaulas "Matemática Zero - Aula 9 - Potenciação", "Matemática Zero - Aula 10 - Radiciação", "Matemática Zero - Aula 11 - Fatoração" e "Matemática Zero - Aula 12 - Racionalização". Todas essas videoaulas estão disponíveis no canal do Nerckie no YouTube:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 3499 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 1817 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- [Radiciação] Raiz dentro de raiz
por amandasousa_m » Sex Jul 19, 2013 09:37
- 2 Respostas
- 2998 Exibições
- Última mensagem por amandasousa_m

Sex Jul 19, 2013 21:58
Equações
-
- como poderia resolver por limites?
por ronaldy » Seg Set 08, 2008 16:22
- 3 Respostas
- 5420 Exibições
- Última mensagem por admin

Ter Set 09, 2008 21:57
Cálculo: Limites, Derivadas e Integrais
-
- limites como resolver sem L'hospital
 por eulercx » Qui Jan 14, 2016 10:37
por eulercx » Qui Jan 14, 2016 10:37
- 1 Respostas
- 3489 Exibições
- Última mensagem por RuuKaasu

Qui Jan 14, 2016 18:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 50 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x} \lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x}](/latexrender/pictures/c75cecf4ecdb298b02d38e536f78ea66.png)


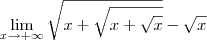
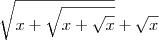 . Nesse caso, temos que:
. Nesse caso, temos que: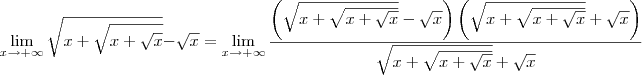
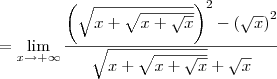

 . Nesse caso, temos que:
. Nesse caso, temos que: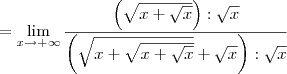
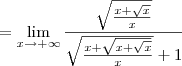

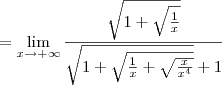
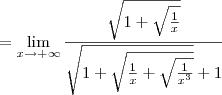

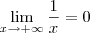
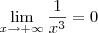
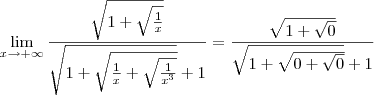

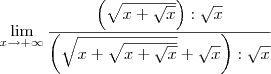
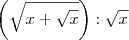 é o mesmo que escrever
é o mesmo que escrever  . Mas lembrando de propriedades de radiciação, sabemos que
. Mas lembrando de propriedades de radiciação, sabemos que  . Desse modo, temos que:
. Desse modo, temos que:
 . Desse modo, podemos escrever que:
. Desse modo, podemos escrever que: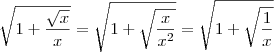


 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: