Como resolver essa questão?
Me deparei com uma questão de uma prova antiga que não estou conseguindo resolver:
" Verifique se existe um número real L tal que a função f definida por
f(x)=![cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right)](/latexrender/pictures/892305de84ef21387bf3e2e208782b9c.png) , se x>0 e
, se x>0 e
f(x)= L, se x=0
é contínua no intervalo [0, + ). "
). "
" Verifique se existe um número real L tal que a função f definida por
f(x)=
![cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right)](/latexrender/pictures/892305de84ef21387bf3e2e208782b9c.png) , se x>0 e
, se x>0 e f(x)= L, se x=0
é contínua no intervalo [0, +
 ). "
). " é continua em
é continua em ![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png) se e só se
se e só se ![\[f(0)=\lim_{x \to 0}f(x)\] \[f(0)=\lim_{x \to 0}f(x)\]](/latexrender/pictures/72e6d29fe38d7ce2a5f838ddb5bf29ef.png) , ou seja,
, ou seja, ![\[L=\lim_{x \to 0}f(x)\] \[L=\lim_{x \to 0}f(x)\]](/latexrender/pictures/ddc8ec56eed64e87853d096eb414dc95.png) .
.
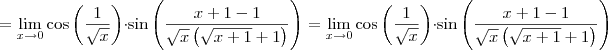

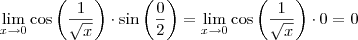


![cos\left(\frac{1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right)](/latexrender/pictures/0bd3dfe730b93b200c4c64156d0c0c8b.png) é limitada, e aplicar o Teorema do Confronto para provar que o limite é igual a zero?
é limitada, e aplicar o Teorema do Confronto para provar que o limite é igual a zero? . Obrigado pela observação.
. Obrigado pela observação.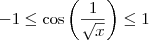 .
.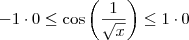 , ou seja,
, ou seja,  .
.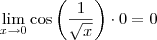 .
.