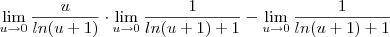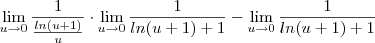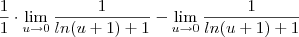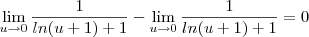joaofonseca escreveu:Seja,

Para encontrar a derivada de f em x=0 faço,
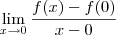
que fica,
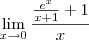
Na verdade, fica:
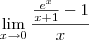
joaofonseca escreveu:Ao substituir obtenho uma indeterminação do tipo, 0/0.
Com a alteração que indiquei acima, de fato temos essa indeterminação.
joaofonseca escreveu:Sei que a técnica de levantamento desta indeterminação passa por fatorar de forma a encontrar o fator comum. Mas eu não estou a ver como fatorar o numerador.
Nesse caso a técnica não é por fatoração.
joaofonseca escreveu:Graficamente já verifiquei que a derivada existe em x=0.
Ok.
joaofonseca escreveu:Podem me dar alguma pista de como começar?
Note que o limite pode ser escrito como:

Agora faça a substituição
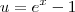
. Desse modo, quando
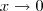
temos que

. Além disso, temos que
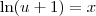
.
Temos então que:
![\lim_{x \to 0} \dfrac{e^x - x - 1}{x(x+1)} = \lim_{u \to 0} \dfrac{u - \ln(u + 1)}{[\ln(u + 1)][\ln(u + 1) + 1]} \lim_{x \to 0} \dfrac{e^x - x - 1}{x(x+1)} = \lim_{u \to 0} \dfrac{u - \ln(u + 1)}{[\ln(u + 1)][\ln(u + 1) + 1]}](/latexrender/pictures/6f4c12d29c0316448abcec2fefcc5097.png)
Agora tente continuar a partir daí.

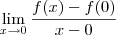



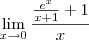
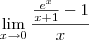

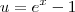 . Desse modo, quando
. Desse modo, quando 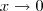 temos que
temos que  . Além disso, temos que
. Além disso, temos que 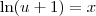 .
.![\lim_{x \to 0} \dfrac{e^x - x - 1}{x(x+1)} = \lim_{u \to 0} \dfrac{u - \ln(u + 1)}{[\ln(u + 1)][\ln(u + 1) + 1]} \lim_{x \to 0} \dfrac{e^x - x - 1}{x(x+1)} = \lim_{u \to 0} \dfrac{u - \ln(u + 1)}{[\ln(u + 1)][\ln(u + 1) + 1]}](/latexrender/pictures/6f4c12d29c0316448abcec2fefcc5097.png)

![\lim_{u\to 0} \frac{u-ln(u+1)}{ln(u+1)[ln(u+1)+1]} \lim_{u\to 0} \frac{u-ln(u+1)}{ln(u+1)[ln(u+1)+1]}](/latexrender/pictures/d3fec2154faf9d307fe061139865e2a8.png)
![\lim_{u\to 0} \frac{u}{ln(u+1)[ln(u+1)+1]}-\lim_{u\to 0}\frac{ln(u+1)}{ln(u+1)[ln(u+1)+1]} \lim_{u\to 0} \frac{u}{ln(u+1)[ln(u+1)+1]}-\lim_{u\to 0}\frac{ln(u+1)}{ln(u+1)[ln(u+1)+1]}](/latexrender/pictures/d4a100a8ddebdd57989dc8b5289963f0.png)