 expressa a quantidade de peças produzidas por um operário em t horas, numa fabrica. Determine:
expressa a quantidade de peças produzidas por um operário em t horas, numa fabrica. Determine:a) a função que da a produção instantânea.
R- "achei" (me disseram) que a resposta é a derivada (
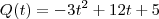 ), contudo, gostaria de uma explicação de porque a simples derivação nos leva a achar produção instantânea?
), contudo, gostaria de uma explicação de porque a simples derivação nos leva a achar produção instantânea?b) para calcular a quantidade de peças produzidas em 2 horas devo simplesmente proceder a resolução da equação? Assim a resposta é:
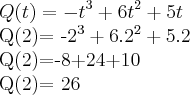
c)Como faço para achar a quantidade Máxima de peças que o operário produz?
Desde já agradeço.


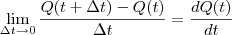 . Ou seja, você pega variações da quantidade de produtos e divide pela variação do tempo. Quando esta variação é muito pequena, ou infinitesimal, diremos que é a derivada.
. Ou seja, você pega variações da quantidade de produtos e divide pela variação do tempo. Quando esta variação é muito pequena, ou infinitesimal, diremos que é a derivada. 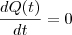 .
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)