Aliocha Karamazov escreveu:Mas, se a derivada de u em relação a x pode ser escrita como
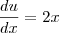
, é só uma questão de notação. Por que, ao "passar dx para o outro lado", a integral é calculada corretamente? Afinal, como
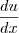
é uma notação, em tese, eu não poderia fazer isso. Não estou duvidando que funciona (porque dá certo!), mas quero saber o porquê.
Como você mesmo disse, a notação
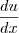
(que é a notação de Leibniz) representa a derivada de u(x). Isto é, representa u'(x).
Usando a definição de derivada, sabemos que:
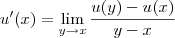
Fazendo a comparação (bem informal) desse limite com a notação de Leibniz, é como se fosse "definido" que:
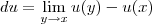
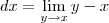
Com essa "definição", temos que

e
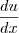
representam o cálculo de um mesmo limite.
Voltando agora para a equação
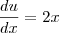
, aplicando a definição de derivada é como se tivéssemos:
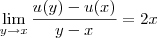
Ignorando por um momento o fato de que

, temos que:


Fazendo uma abstração (bem informal), esse resultado poderia ser obtido diretamente "passando o dx para o outro lado" na equação original.
Essa é mais ou menos a ideia por trás dessa operação que fazemos.
Mas note que tudo que escrevi foi informal.
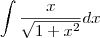

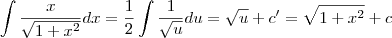
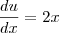 , é só uma questão de notação. Por que, ao "passar dx para o outro lado", a integral é calculada corretamente? Afinal, como
, é só uma questão de notação. Por que, ao "passar dx para o outro lado", a integral é calculada corretamente? Afinal, como 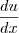 é uma notação, em tese, eu não poderia fazer isso. Não estou duvidando que funciona (porque dá certo!), mas quero saber o porquê. Obrigado.
é uma notação, em tese, eu não poderia fazer isso. Não estou duvidando que funciona (porque dá certo!), mas quero saber o porquê. Obrigado.

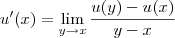
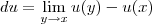
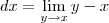
 e
e 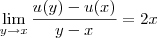
 , temos que:
, temos que:


 como uma forma diferencial, dando um sentido então a isto.
como uma forma diferencial, dando um sentido então a isto.


 , avisa que eu resolvo.
, avisa que eu resolvo.

