 por cal12 » Sáb Nov 26, 2011 17:52
por cal12 » Sáb Nov 26, 2011 17:52
-
cal12
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Ago 14, 2011 11:21
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por LuizAquino » Sáb Nov 26, 2011 18:13
por LuizAquino » Sáb Nov 26, 2011 18:13
cal12 escreveu:Gostaria de saber como fazer estas questões por L'Hospital pois estou fazendo e não estão batendo com o resultado que me foi informado.
Para estudar a resolução de cada um desses limites, siga o procedimento abaixo.
Vale lembrar que esse procedimento irá aplicar a Regra de L'Hospital sempre que puder.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
limit (2x^3 - x - 1)/(x^4 - 1) as x-> 0
- Clique no botão de igual ao lado do campo de entrada.
- Após o limite ser calculado, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução e comparar com a sua.
Vale lembrar que para cada limite você precisa alterar o passo 2 de forma conveniente.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- l'hospital
por vinicastro » Dom Dez 16, 2012 16:32
- 1 Respostas
- 1515 Exibições
- Última mensagem por vinicastro

Dom Dez 16, 2012 17:15
Cálculo: Limites, Derivadas e Integrais
-
- L'Hospital
por matmatco » Sáb Fev 23, 2013 16:35
- 1 Respostas
- 1629 Exibições
- Última mensagem por LuizAquino

Ter Fev 26, 2013 17:09
Cálculo: Limites, Derivadas e Integrais
-
- L'Hospital
por duduxo81 » Sex Jul 08, 2016 11:30
- 3 Respostas
- 5264 Exibições
- Última mensagem por duduxo81

Qua Jul 13, 2016 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 20:26
- 2 Respostas
- 1916 Exibições
- Última mensagem por Claudin

Qui Jul 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 21:16
- 9 Respostas
- 3341 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 16, 2011 15:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\lim_{x\rightarrow1}\left[\frac{1}{ln(x)}-\frac{1}{x-1} \right]= \lim_{x\rightarrow1}\left[\frac{1}{ln(x)}-\frac{1}{x-1} \right]=](/latexrender/pictures/e149c843b2901ade478d3af3cf560af7.png)

![\lim_{x\rightarrow1}\frac{\sqrt[3]{1+2x+1}}{x+\sqrt[2]{2+x}}= \lim_{x\rightarrow1}\frac{\sqrt[3]{1+2x+1}}{x+\sqrt[2]{2+x}}=](/latexrender/pictures/216c66170c5fc75b153c7b8f4c5cfba7.png)
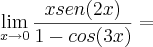


![\lim_{x\rightarrow1}\left[\frac{1}{ln(x)}-\frac{1}{x-1} \right]= \lim_{x\rightarrow1}\left[\frac{1}{ln(x)}-\frac{1}{x-1} \right]=](/latexrender/pictures/e149c843b2901ade478d3af3cf560af7.png)

![\lim_{x\rightarrow1}\frac{\sqrt[3]{1+2x+1}}{x+\sqrt[2]{2+x}}= \lim_{x\rightarrow1}\frac{\sqrt[3]{1+2x+1}}{x+\sqrt[2]{2+x}}=](/latexrender/pictures/216c66170c5fc75b153c7b8f4c5cfba7.png)
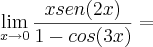




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.