 por carvalhothg » Qua Nov 23, 2011 12:04
por carvalhothg » Qua Nov 23, 2011 12:04
Como resolvo este limite para encontrar os valores de a e b. Não estou conseguindo, sempre chego na indeterminação de

- Se
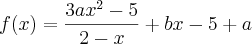
, calcule a e b de modo que:
1)
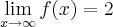
2)
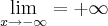
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] Me ajudem
por carvalhothg » Qua Nov 16, 2011 16:52
- 2 Respostas
- 1253 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 19:26
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES ME AJUDEM POR FAVOR URGENTE
por gaahbr » Qui Nov 07, 2013 11:47
- 0 Respostas
- 1930 Exibições
- Última mensagem por gaahbr

Qui Nov 07, 2013 11:47
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5409 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4755 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4783 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

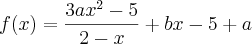 , calcule a e b de modo que:
, calcule a e b de modo que: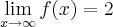
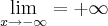


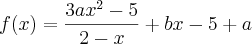 , calcule a e b de modo que:
, calcule a e b de modo que: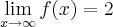
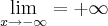

, calcule a e b de modo que:
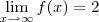
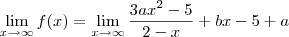
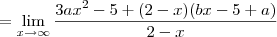
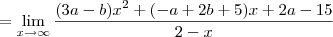
![\lim_{x\to \infty} \frac{(- a + 2b + 5)x + 2a - 15}{2-x} = \lim_{x\to \infty} \frac{[(- a + 2b + 5)x + 2a - 15]:x}{(2-x):x} \lim_{x\to \infty} \frac{(- a + 2b + 5)x + 2a - 15}{2-x} = \lim_{x\to \infty} \frac{[(- a + 2b + 5)x + 2a - 15]:x}{(2-x):x}](/latexrender/pictures/510cc53bdff32e22684e38d72ddf7cc9.png)
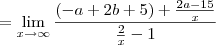
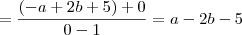
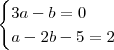
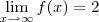
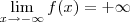
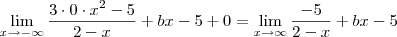
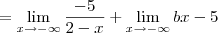
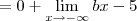
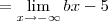
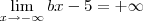
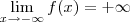

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.