 por manolo223 » Seg Nov 14, 2011 14:37
por manolo223 » Seg Nov 14, 2011 14:37
mostrar que a equaçao cos(y)y'+2xsen(y)=-2x pode ser transformada numa equaçao linear e resolver o PVI y(0)=0
eu tentei fazer o seguinte:
chamar de k=sen(y)
derivar k em funçao de y , dk/dy = cos(y)
(dk/dy).y' + 2xk = -2x
(dk/dy).(dy/dx) + 2xk = -2x <=> dk/dx + 2xk = -2x => k' + 2xk = -2x
nao sei se poderia fazer isso , mas caso fosse possivel como faria com respeito ao y(0)=0 nao tenho valor de z para jogar na equaçao depois de aplicar a regra. alguem tem uma ideia de como resolver?
-
manolo223
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Nov 13, 2011 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: física/engenharia
- Andamento: cursando
 por MarceloFantini » Seg Nov 14, 2011 19:12
por MarceloFantini » Seg Nov 14, 2011 19:12
Não me lembro muito de EDO, mas não seria possível usar a transformada de Laplace?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Seg Nov 14, 2011 20:29
por LuizAquino » Seg Nov 14, 2011 20:29
manolo223 escreveu:chamar de k=sen(y)
A variável y está em função de x. Temos então que
k também está em função de x.
manolo223 escreveu:como faria com respeito ao y(0)=0
Note que:
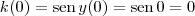
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por manolo223 » Ter Nov 15, 2011 00:45
por manolo223 » Ter Nov 15, 2011 00:45
falta de atenção minha, percebi isso pouco depois de fazer a pergunta . Obrigado pelo exclarecimento
-
manolo223
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Nov 13, 2011 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: física/engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10717 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9728 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3314 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4609 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6531 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
.