 por luanalcs » Qui Nov 10, 2011 06:22
por luanalcs » Qui Nov 10, 2011 06:22
Pessoal
Estou tendo dificuldades para esboçar o gráfico da função a seguir:
f(x)=2x³+x-2
1º Passo: Derivada
f'(x)=6x²+1
2º Passo: Pontos críticos (mínimos e máximos)
f'(x)=0
6x²+1=0
6x²=-1
x²=-1/6
x=+-1/6
3º Passo: Determinar pontos críticos
x= 1/6
f(x)=2x³+x-2
2*(0,1666)³+(0,1666)-2= 7 (1/6,7)
x= (-1/6)
f(x)=2x³+x-2
2*(-0,1666)³+(-0,1666)-2= -11 (1/6,-11)
4º Passo: Segunda derivada da função
f(x)=6x²+1
f"(x)=12x
5º Passo: Definir concavidade no ponto crítico
x= 1/6
f"(1/6)=12*1/6= 2 (Para cima)
x= -1/6
f"(-1/6)=12*(-1/6)= -2 (Para baixo)
6º Passo: Ponto de inflexão
f"(x)=0
12x=0
x=0
f(x)=2x³+x-2
f(0)= 2*0³+0-2= -2
Creio que esteja errada a montagem do gráfico, marquei (-1/6,-11) (1/6,7) (0,2).
Não consigo vizualizar aonde possa estar o erro.
Desde já agradeço
Editado pela última vez por
luanalcs em Qui Nov 10, 2011 18:53, em um total de 1 vez.
-
luanalcs
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Nov 10, 2011 05:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Economicas
- Andamento: cursando
 por joaofonseca » Qui Nov 10, 2011 08:14
por joaofonseca » Qui Nov 10, 2011 08:14
O erro está nos zeros da derivada.

Não tem zeros reais.O vertice da parabola será um minimo.Com alguma atenção se verifica que a função pode ser escrita da seguite forma:

em que
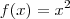
. Podemos concluir que o vertice da função elementar sofreu uma deslocação de 1 unidade para cima.Assim de (0,0) passou para (0,1). O fator de expanção 6, não afeta em nada o vertice da parabola.
Concluimos que se o minimo da parabola é (0,1) então não há zeros.Se a derivada não tem zeros e é positiva em todo o seu dominio, f(x) é estritamente crescente.
Todos os calculos posteriores que utilizam as falsas raizes da derivada estam errados.
Aqui fica uma fotografia:

- derivadas.jpg (15.1 KiB) Exibido 1581 vezes
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qui Nov 10, 2011 11:58
por LuizAquino » Qui Nov 10, 2011 11:58
Olá
joaofonseca e
luanalcs,
Já que a dúvida foi resolvida, gostaria apenas de deixar uma sugestão. Trata-se do programa GeoGebra, que com certeza pode ajudar muito nos seus estudos.
A página oficial desse programa é:
http://www.geogebra.orgSe vocês desejarem, no meu canal no YouTube tem um conjunto de tutoriais sobre esse programa. O endereço é:
http://www.youtube.com/LCMAquinoEm particular, eu recomendo o vídeo tutorial "10. Curso de GeoGebra - Funções".
Por fim, se vocês precisarem fazer uma revisão, no meu canal também há uma vídeo-aula tratando sobre a construção de gráficos: "22. Cálculo I - Construção de Gráficos".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Gráfico de Derivada
por Bruhh » Qui Jun 17, 2010 14:43
- 0 Respostas
- 1356 Exibições
- Última mensagem por Bruhh

Qui Jun 17, 2010 14:43
Cálculo: Limites, Derivadas e Integrais
-
- Esboço do gráfico de derivada
por luiz3107 » Qua Ago 18, 2010 16:28
- 0 Respostas
- 2054 Exibições
- Última mensagem por luiz3107

Qua Ago 18, 2010 16:28
Cálculo: Limites, Derivadas e Integrais
-
- [derivada]contrução de grafico
por giulioaltoe » Qua Ago 17, 2011 19:46
- 1 Respostas
- 988 Exibições
- Última mensagem por LuizAquino

Qua Ago 17, 2011 22:52
Cálculo: Limites, Derivadas e Integrais
-
- Derivada reta tangente ao gráfico
por Carolminera » Dom Jul 06, 2014 16:53
- 1 Respostas
- 2630 Exibições
- Última mensagem por e8group

Dom Jul 06, 2014 20:11
Cálculo: Limites, Derivadas e Integrais
-
- Derivada reta tangente ao gráfico
por Carolminera » Qua Jul 23, 2014 11:33
- 1 Respostas
- 1755 Exibições
- Última mensagem por Russman

Qua Jul 23, 2014 21:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 em que
em que 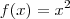 . Podemos concluir que o vertice da função elementar sofreu uma deslocação de 1 unidade para cima.Assim de (0,0) passou para (0,1). O fator de expanção 6, não afeta em nada o vertice da parabola.
. Podemos concluir que o vertice da função elementar sofreu uma deslocação de 1 unidade para cima.Assim de (0,0) passou para (0,1). O fator de expanção 6, não afeta em nada o vertice da parabola.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.