Olá pessoal, gostaria novamente de agradecer pela ajuda nos tópicos anteriores.
Hoje trago 2 questões para determinação do lucro máximo, a primeira:
1) Uma certa indústria vende seu produto por R$ 100,00 a unidade. Se o custo da produção total diária, em R$, para x unidades for C(x) = 0,0025x² + 50x + 100.000 e se a capacidade de produção mensal for, de no máximo, 15000 unidades, quantas unidades desse produto devem ser fabricadas e vendidas mensalmente para que o lucro seja máximo?
Eu conseguir resolve-lá considerando venda = 100x e C(x). Logo L(x) 100x - C(x)
Para obter lucro máximo L'(x) = 0 e L"(x) < 0
Derivei a função L e encontrei o resultado de 10.000 unidades. Gostaria de saber se fiz corretamente.
Já a segunda questão tentei resolver pelo mesmo método porém não obtive exito.
2) Uma empresa opera num mercado em que o preço de venda é constante e igual a $20. seu custo marginal mensal é dado por 3x2 – 6x + 15 qual a produção que dá o máximo lucro. (a própria questão veio com 3x2, porém acredito que seja 3x²)
Gostaria de uma ajuda para resolve-lá.
Desde já agradeço.


 .
.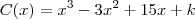 (onde
(onde  .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)