Boa tarde,
alguém poderia me ajudar a resolver tal exercício?
Determine uma família de funções que verifique a equação : x. df/dx + y df/dy = o
Exercício retirado do livro Guidorizzi de cálculo II - pág 226 // regra dacadeia
Obrigado.





 .
.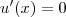 basta que u(x) seja uma função contante, já que a derivada de uma constante é zero.Mas se u(x) for uma constante já não estamos perante uma função composta. Na pratica estariamos a calcular a derivada de f(x) num ponto da função f (declive da reta tangente).
basta que u(x) seja uma função contante, já que a derivada de uma constante é zero.Mas se u(x) for uma constante já não estamos perante uma função composta. Na pratica estariamos a calcular a derivada de f(x) num ponto da função f (declive da reta tangente).
carlosmarinio escreveu:Determine uma família de funções que verifique a equação : x. df/dx + y df/dy = 0
Exercício retirado do livro Guidorizzi de cálculo II - pág 226 // regra dacadeia
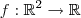 tal que f seja homogênea de grau 0.
tal que f seja homogênea de grau 0.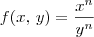 verifica a equação dada.
verifica a equação dada.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: