 , onde
, onde 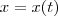 é uma função derivável. Calcule
é uma função derivável. Calcule  no ponto t=1, supondo
no ponto t=1, supondo  no ponto t=1 e
no ponto t=1 e 
Eu pensei em fazer assim:
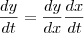 .
.Como eu já tenho

Só preciso calcular
 . Então:
. Então:
Mas, nesse caso, eu tenho que derivar em relação a x, certo? Ficaria apenas
 . Não entendi por que o exercício deu
. Não entendi por que o exercício deu  .
.O exercício parece ser bem simples, é que eu não entendi direito mesmo. Alguém poderia me ajudar?


 , supondo
, supondo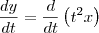

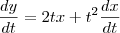
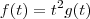
![f^\prime(t) = [t^2g(t)]^\prime f^\prime(t) = [t^2g(t)]^\prime](/latexrender/pictures/1cbcdc715bf54ac547e86aee5a098dd7.png)
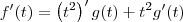

 sabendo-se que
sabendo-se que 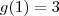 e
e 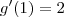 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)