 por Keleber » Sex Out 21, 2011 15:04
por Keleber » Sex Out 21, 2011 15:04
Oi para todos. Sou novo aqui, mas em geral eu não sou novo em outro lugar.
O que eu queria saber é o seguinte, suponhamos que temos a derivada dy/dx, e que por uma serie de procedimentos ela venha se tornar, por exemplo, algo como
dh/dsen(xf), ou dy/logx, ou algo parecido.
Como se resolve derivadas deste tipo? isto é, que tenham um diferencial composto, semelhante a uma equação?
O mesmo acontece com as integrais, como resolve-las? Quando o diferencial não é uma simples variavel?
-
Keleber
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 21, 2011 14:47
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Física
- Andamento: cursando
 por Neperiano » Sex Out 21, 2011 15:29
por Neperiano » Sex Out 21, 2011 15:29
Ola
No caso de derivadas eu não sei, no caso de integrais quando você tem por exemplo y' = xlog (x), você pode fazer por variaveis separadas, tipo: Integral de dy = Integral de (x log x)dx
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por joaofonseca » Sex Out 21, 2011 16:37
por joaofonseca » Sex Out 21, 2011 16:37
Será que te estás a referir à derivada de uma função composta?
Por exemplo:
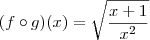
Em que
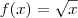
e

. Neste caso aplica-se a regra da cadeia (chain rule).
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Keleber » Sex Out 21, 2011 19:33
por Keleber » Sex Out 21, 2011 19:33
É possivel que seja função composta, mas eu não tenho certeza.
Por exemplo, eu parto de duas hipóteses,:
Primeiro, a função do tipo df(g(x))/dg(x) se resolveria assim, por exemplo: d((x^2)^3/d(x^2) = 3(x^2)^2. A outra forma seria por, como disse o colega, regra da cadeia.| |(|^|.|^|)| |
-
Keleber
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 21, 2011 14:47
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Sáb Out 22, 2011 00:35
por LuizAquino » Sáb Out 22, 2011 00:35
Keleber escreveu:Primeiro, a função do tipo df(g(x))/dg(x) (...)
Não se usa essa notação dessa maneira.
Considere que você tenha a composição y = f(g(x)). Fazendo a substituição u = g(x), a composição passa a ser escrita simplesmente como y = f(u).
Usando a notação que você deseja (conhecida como
notação de Leibniz), a derivada dessa composição seria representada por:
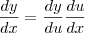
Usando a notação de "linha" (ou notação de Lagrange), essa mesma derivada seria representada por:
![[f(g(x))]^\prime = f^\prime(g(x))g^\prime(x) [f(g(x))]^\prime = f^\prime(g(x))g^\prime(x)](/latexrender/pictures/43b700ef86b2f826eb9f4de60fe885f5.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Juros Composto] Desconto comercial composto
por DPassos » Qui Mar 05, 2015 18:18
- 2 Respostas
- 5716 Exibições
- Última mensagem por Russman

Sex Mar 06, 2015 00:37
Matemática Financeira
-
- [Diferencial] Diferencial total
por temujin » Qua Mai 29, 2013 17:10
- 2 Respostas
- 1257 Exibições
- Última mensagem por temujin

Ter Out 21, 2014 17:17
Cálculo: Limites, Derivadas e Integrais
-
- Juros Composto
por EderPachecoLopes » Sex Fev 19, 2010 18:40
- 2 Respostas
- 3327 Exibições
- Última mensagem por Cleyson007

Sáb Fev 20, 2010 18:56
Matemática Financeira
-
- [Desconto Composto]
por GMartins » Seg Abr 02, 2012 11:15
- 1 Respostas
- 1530 Exibições
- Última mensagem por Fabiano Vieira

Sáb Abr 21, 2012 22:19
Matemática Financeira
-
- Juros Composto
por Catia Fernanda » Sex Abr 10, 2015 16:00
- 1 Respostas
- 4251 Exibições
- Última mensagem por Baltuilhe

Ter Jun 30, 2015 18:13
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



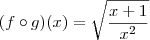
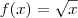 e
e  . Neste caso aplica-se a regra da cadeia (chain rule).
. Neste caso aplica-se a regra da cadeia (chain rule).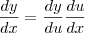
![[f(g(x))]^\prime = f^\prime(g(x))g^\prime(x) [f(g(x))]^\prime = f^\prime(g(x))g^\prime(x)](/latexrender/pictures/43b700ef86b2f826eb9f4de60fe885f5.png)

