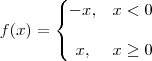por isso estou aqui postando minhas duas dúvidas por enquanto:
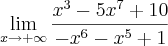
![\lim_{x\rightarrow +\infty}\frac{\sqrt[2]{x^2+1}}{3x+2} \lim_{x\rightarrow +\infty}\frac{\sqrt[2]{x^2+1}}{3x+2}](/latexrender/pictures/7f7eee5372d8be1135c5f6736c82138d.png)
bom no primeiro caso eu comecei tentando divisão de polinômios, mas me enrolei..
aí tentei dividir o numerado e o denominador pelo fator de maior grau, no caso x^7; só que aí no denominador ficaria 0, já que todos os fatores iriam tender a 0;
briot rufini eu nem tentei e não sei nem como começar a fatorar esse negócio...
no segundo caso, tentei usar o conjugado, mas não cheguei em lugar nenhum e multiplicar por um fator igual a 1 tbm não deu em nada..
não sei o que fazer..
se eu conseguir entender esses dois casos, já é metade do caminho andado pra eu entender a lista que tenho que resolver..
obrigado


 .Basta observar que o grau do numerado é maior que o grau do denominador. Se o sinal negativo dos coeficientes de maior grau atrapalham, experimenta tira-los para fora, alterando os sinais dos restantes termos.
.Basta observar que o grau do numerado é maior que o grau do denominador. Se o sinal negativo dos coeficientes de maior grau atrapalham, experimenta tira-los para fora, alterando os sinais dos restantes termos. e que se
e que se  então podemo-nos limitar à parte positiva de
então podemo-nos limitar à parte positiva de  , ou seja
, ou seja 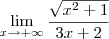
 e o denominador por
e o denominador por 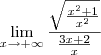
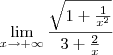




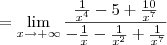
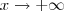 , temos que o numerador dessa fração tende para -5, enquanto que o denominador tende para 0 (porém se aproximando por valores negativos). Desse modo, o resultado final será:
, temos que o numerador dessa fração tende para -5, enquanto que o denominador tende para 0 (porém se aproximando por valores negativos). Desse modo, o resultado final será: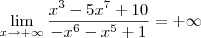

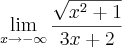
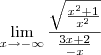
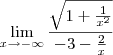

 estaria certo?
estaria certo?