 por valeuleo » Seg Out 03, 2011 11:59
por valeuleo » Seg Out 03, 2011 11:59
Tentei resolver as seguintes questões e gostaria que analisassem se as resoluções (resultados e procedimentos) estão corretos. Segue:
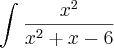
Sabendo que:

Tenho que:

Então:
![\int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx \int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx](/latexrender/pictures/4ab67acf64b5dea9213f4a72efe335d2.png)
Fazendo A e B:
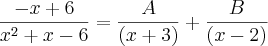

Fazendo x=2, obtemos B = 4/5 e com x=-3 obtemos A=-9/5
Fazendo as integrais:

Temos então:
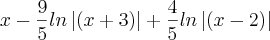
(Depois posto as outras resoluções)
Grato
-
valeuleo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Mar 23, 2011 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: cursando
 por LuizAquino » Seg Out 03, 2011 16:11
por LuizAquino » Seg Out 03, 2011 16:11
Ao invés de "ganhar o peixe", que tal "aprender a pescar"?
Para conferir a sua resolução, siga os passos:
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (x^2)/(x^2+x-6) dx
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Basta conferir a resolução.
ObservaçãoObviamente, a resolução pode variar um pouco em relação a sua.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por valeuleo » Seg Out 03, 2011 16:40
por valeuleo » Seg Out 03, 2011 16:40
Esse site resolve de uma maneira "não acadêmica rsrs". O meu deu diferente, mas os procedimentos da página são outros.
-
valeuleo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Mar 23, 2011 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: cursando
 por LuizAquino » Seg Out 03, 2011 17:16
por LuizAquino » Seg Out 03, 2011 17:16
valeuleo escreveu:Esse site resolve de uma maneira "não acadêmica rsrs". O meu deu diferente, mas os procedimentos da página são outros.
Não "acadêmica"?! A integral foi resolvida aplicando o método das frações parciais da mesma forma que você fez!
A técnica foi aplicada logo no início:
For the integrand
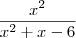
, do long division:
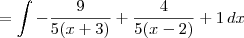
Eis a resposta final indicada na página:
Sendo que na própria página há um aviso:

is the natural logarithm
Considerando-se que onde há parênteses na solução o que temos na verdade são módulos e que nessa página

representa
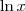
, a solução apresentada é a mesma que a sua!
ObservaçãoLembre-se que |x - 2| = |2 - x|.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por valeuleo » Seg Out 03, 2011 17:31
por valeuleo » Seg Out 03, 2011 17:31
Obrigado... eu tinha esquecido do "integrate"
-
valeuleo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Mar 23, 2011 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas/Integrais] Ajuda com 5 questões de cálculo
por matheuskns » Sex Nov 28, 2014 20:27
- 1 Respostas
- 1878 Exibições
- Última mensagem por Cleyson007

Sáb Nov 29, 2014 20:40
Cálculo: Limites, Derivadas e Integrais
-
- Correção Polinômios
por Cleyson007 » Dom Jan 24, 2010 09:56
- 1 Respostas
- 1677 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 06, 2010 20:39
Polinômios
-
- Correção Polinômios II
por Cleyson007 » Dom Jan 24, 2010 10:14
- 5 Respostas
- 3440 Exibições
- Última mensagem por DanielFerreira

Seg Mar 15, 2010 04:53
Polinômios
-
- Correção Polinômios III
por Cleyson007 » Dom Jan 24, 2010 11:00
- 1 Respostas
- 1713 Exibições
- Última mensagem por vyhonda

Sex Fev 12, 2010 15:18
Polinômios
-
- Correção Polinômios IV
por Cleyson007 » Dom Jan 24, 2010 11:04
- 0 Respostas
- 1148 Exibições
- Última mensagem por Cleyson007

Dom Jan 24, 2010 11:04
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
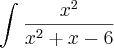


![\int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx \int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx](/latexrender/pictures/4ab67acf64b5dea9213f4a72efe335d2.png)
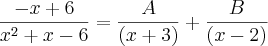


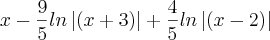

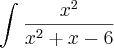


![\int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx \int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx](/latexrender/pictures/4ab67acf64b5dea9213f4a72efe335d2.png)
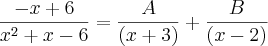


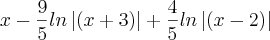



, do long division:
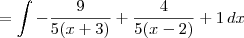
is the natural logarithm
 representa
representa 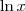 , a solução apresentada é a mesma que a sua!
, a solução apresentada é a mesma que a sua!






