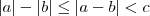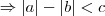-civil- escreveu:Eu resolvi assim:
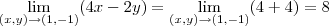
(Posso considerar que esse é um jeito de resolver por caminho?)
Claro que
não! Afinal de contas, você
não especificou que caminho você está seguindo!
Uma forma seria, por exemplo, considerar que você vai se aproximar do ponto (1, -1) seguindo a trajetória da reta y = -x. Note que seguindo essa trajetória, quando x se aproxima de 1, temos que y se aproxima de -1. Sobre essa trajetória, o limite acima é o mesmo que:

-civil- escreveu:Seja
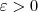
, queremos achar

tal que
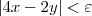
sempre que

Não é isso. Considerando que você desconfia que o limite seja igual a 6, então o que você quer é tentar provar que:
Seja 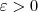 , queremos achar
, queremos achar  tal que
tal que 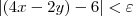 sempre que
sempre que  .
.-civil- escreveu:
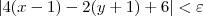
Não é isso. O que temos é:
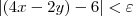


Mas pela desigualdade triangular, sabemos que:
![|4(x-1) + [-2(y+1)]| \leq |4(x-1)| + |-2(y+1)| |4(x-1) + [-2(y+1)]| \leq |4(x-1)| + |-2(y+1)|](/latexrender/pictures/65718870a2911ba6c60a0626854e02d7.png)

Em resumo, temos que:
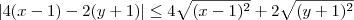
Por outro lado, sabemos que:
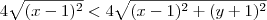
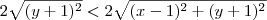
Ou seja, é válido que:

Desse modo, podemos afirmar que:
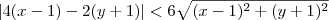
Isso significa que podemos escolher
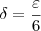
.
Agora, verifique que essa escolha é conveniente.
Observação-civil- escreveu: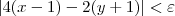
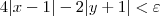
(Eu posso fazer isso, tendo um sinal negativo ali no meio????)
Ao que parece, você executou esse passo pensando que é válido a propriedade |a - b| = |a| - |b|, para quaisquer a e b reais. Entretanto, isso é claramente inválido. Escolha, por exemplo, a = 1 e b = -1. Você perceberá que essa relação é inválida para essa escolha.
A propriedade que de fato nós temos é

, para quaisquer a e b reais . Para uma demonstração dessa propriedade, vide o tópico:
Re: Módulo.viewtopic.php?f=120&t=4101#p13503Considerando agora essa propriedade, se tivermos algo do tipo

(com
c positivo e não nulo), como

, então podemos afirmar que:
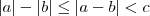
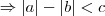
Em resumo, devido a essa propriedade, para quaisquer a, b e c reais (com c positivo e não nulo) temos que:

 em função de
em função de  , o valor do
, o valor do  e finalmente a confirmação de
e finalmente a confirmação de  .
.
 =
= 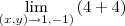 = 8
= 8 > 0, queremos achar
> 0, queremos achar  tal que |4x - 2y| <
tal que |4x - 2y| <  sempre que
sempre que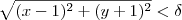
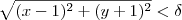
 = | x - 1 | <
= | x - 1 | < 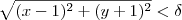 --->>>> projeto de
--->>>> projeto de 
 = | y + 1| <
= | y + 1| < 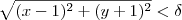



 (Eu posso fazer isso, tendo um sinal negativo ali no meio????)
(Eu posso fazer isso, tendo um sinal negativo ali no meio????) - 2
- 2 <
< 
 <
< 
 :
: 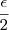
 :
: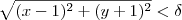 então
então e | y + 1| <
e | y + 1| < 
 - 2
- 2 < 2
< 2
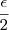
 4|x-1| - 2|y+1|
4|x-1| - 2|y+1|


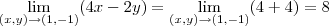

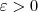 , queremos achar
, queremos achar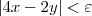 sempre que
sempre que
 tal que
tal que 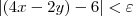 sempre que
sempre que 
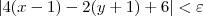


![|4(x-1) + [-2(y+1)]| \leq |4(x-1)| + |-2(y+1)| |4(x-1) + [-2(y+1)]| \leq |4(x-1)| + |-2(y+1)|](/latexrender/pictures/65718870a2911ba6c60a0626854e02d7.png)

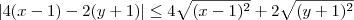
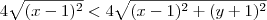
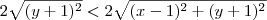

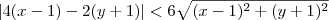
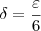 .
.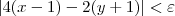
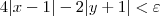
 , para quaisquer a e b reais . Para uma demonstração dessa propriedade, vide o tópico:
, para quaisquer a e b reais . Para uma demonstração dessa propriedade, vide o tópico: (com
(com  , então podemos afirmar que:
, então podemos afirmar que: