 por Anderson Silva » Dom Set 18, 2011 14:56
por Anderson Silva » Dom Set 18, 2011 14:56
Como calcular a área da região limitada pelo gráfico da função y = x elevado a 3 e pela reta y = 3x - 2 , que é tangente à curva y = x elevado a 3 no ponto (1,1).
Obs: Encontrei onde as funções se interceptam(pontos -2 e 1), mas estou com dúvidas na conclusão do exercício pois achei o resultado 11/4 u.a. mas ao conferir a resposta encontrei o resultado 27/4 u.a. Gostaria de saber onde errei.
Grato desde já.
-
Anderson Silva
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Set 18, 2011 14:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Dom Set 18, 2011 17:53
por LuizAquino » Dom Set 18, 2011 17:53
Anderson Silva escreveu:Gostaria de saber onde errei.
Como podemos dizer se você não enviou a sua resolução? Você determinou a interseção entre os gráficos de forma adequada. Provavelmente você se atrapalhou no cálculo da integral.
Note que o gráfico de

está acima da reta
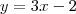
no intervalo [-2, 1]. Isto é, temos que
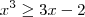
para valores de x no intervalo [-2, 1].
Isso significa que a área delimitada será dada por:
![\int_{-2}^1 x^3 - (3x-2)\,dx = \left[\frac{x^4}{4} - \frac{3x^2}{2} + 2x\right]_{-2}^1 \int_{-2}^1 x^3 - (3x-2)\,dx = \left[\frac{x^4}{4} - \frac{3x^2}{2} + 2x\right]_{-2}^1](/latexrender/pictures/911e89bd9e33df9f97c7957ea57bea95.png)
![= \left(\frac{1^4}{4} - \frac{3\cdot 1^2}{2} + 2\cdot 1\right) - \left[\frac{(-2)^4}{4} - \frac{3\cdot (-2)^2}{2} + 2\cdot (-2)\right] = \frac{27}{4} = \left(\frac{1^4}{4} - \frac{3\cdot 1^2}{2} + 2\cdot 1\right) - \left[\frac{(-2)^4}{4} - \frac{3\cdot (-2)^2}{2} + 2\cdot (-2)\right] = \frac{27}{4}](/latexrender/pictures/22fac1b71c0b5d5e2a5d72c74c184808.png) Observação
ObservaçãoProcure digitar as notações matemáticas usando o LaTeX. Leia o tópico falando a respeito:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74Se precisar, use também o
Editor de Fórmulas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas em exercício logarítmico
por Filipefutsal » Seg Jun 24, 2013 08:46
- 2 Respostas
- 2216 Exibições
- Última mensagem por Filipefutsal

Seg Jun 24, 2013 14:53
Funções
-
- [Conjuntos] Dúvidas no exercício.
por HeidyTrinidad » Sex Abr 11, 2014 10:35
- 1 Respostas
- 1803 Exibições
- Última mensagem por e8group

Sex Abr 11, 2014 18:16
Conjuntos
-
- [Limites] Dúvidas no exercício. Me ajude na Resolução.
 por Thamiires » Ter Nov 29, 2011 21:18
por Thamiires » Ter Nov 29, 2011 21:18
- 1 Respostas
- 1660 Exibições
- Última mensagem por TheoFerraz

Ter Nov 29, 2011 22:30
Cálculo: Limites, Derivadas e Integrais
-
- Tenho duvidas de como resolver este exercício!!!!
por Sarah_bernadeth » Sex Mar 28, 2008 18:47
- 1 Respostas
- 2212 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 20:02
Álgebra Elementar
-
- Tenho dúvidas de como resolver este exercício de conjuntos
por Thiago Sousa » Ter Mai 06, 2008 17:11
- 2 Respostas
- 4570 Exibições
- Última mensagem por Thiago Sousa

Ter Mai 06, 2008 19:25
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 está acima da reta
está acima da reta 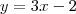 no intervalo [-2, 1]. Isto é, temos que
no intervalo [-2, 1]. Isto é, temos que 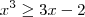 para valores de x no intervalo [-2, 1].
para valores de x no intervalo [-2, 1].![\int_{-2}^1 x^3 - (3x-2)\,dx = \left[\frac{x^4}{4} - \frac{3x^2}{2} + 2x\right]_{-2}^1 \int_{-2}^1 x^3 - (3x-2)\,dx = \left[\frac{x^4}{4} - \frac{3x^2}{2} + 2x\right]_{-2}^1](/latexrender/pictures/911e89bd9e33df9f97c7957ea57bea95.png)
![= \left(\frac{1^4}{4} - \frac{3\cdot 1^2}{2} + 2\cdot 1\right) - \left[\frac{(-2)^4}{4} - \frac{3\cdot (-2)^2}{2} + 2\cdot (-2)\right] = \frac{27}{4} = \left(\frac{1^4}{4} - \frac{3\cdot 1^2}{2} + 2\cdot 1\right) - \left[\frac{(-2)^4}{4} - \frac{3\cdot (-2)^2}{2} + 2\cdot (-2)\right] = \frac{27}{4}](/latexrender/pictures/22fac1b71c0b5d5e2a5d72c74c184808.png)



 , avisa que eu resolvo.
, avisa que eu resolvo.

