Neperiano escreveu:Você tenque calcular a integral dessa equação (...)
Não faz sentido falar em integral de uma
equação, mas sim em integral de uma
função.
Quando temos uma
equação, dependendo do contexto, o que podemos fazer é integrar ambos os seus membros. Nesse caso, estamos enxergando a expressão em cada membro como se fosse uma
função em relação a alguma variável.
bencz escreveu:tenho a função
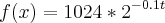
Ao que parece você deseja que a variável independente da função seja t. Desse modo, o correto seria escrever:

bencz escreveu:Ponto1: (T = 0 ; f(t) = 1024)
Ponto2: (T = 14; f(t) = 64}
De fato, f(0) é igual a 1024. Mas, f(14) não é igual 64. Na verdade, f(40) é igual 64. Confira os dados do exercício.
bencz escreveu:Bom, gostaria de saber, como posso fazer para calcular a area abaixo dessa curva
No caso, você deseja a área entre o gráfico de f e o eixo x no intervalo [0, 40]. Para isso, basta calcular:

Para resolver essa integral, use a técnica de substituição. Faça

e

.
Perceba que se

, temos que

. Por outro lado, se

, temos que

.
Desse modo, podemos reescrever essa integral como:
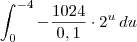
Agora tente terminar de resolver o exercício.
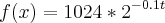





 e
e  .
. , temos que
, temos que  . Por outro lado, se
. Por outro lado, se  , temos que
, temos que  .
.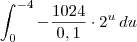


 .
.
 :
: