 por ewald » Sáb Ago 20, 2011 17:20
por ewald » Sáb Ago 20, 2011 17:20
Oi, nao consigo fazer esta questao (logo abaixo). Eu sei que devo usar as relaçoes sen²x = (1 - cos2x)/2 e cos²x = (1 + cos2x)/2 mas chega um ponto que ela fica gigante e o que é pior o resultado nao sai igual ao do gabarito. Bem se alguem puder resolver pra mim eu agradeço.

[integral indef. de 48 vezes seno ao quadrado de x vezes coseno elevado a quarta potencia de x]
Obrigado
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por ewald » Sáb Ago 20, 2011 20:02
por ewald » Sáb Ago 20, 2011 20:02
Consegui!!

Obrigado pra quem leu e tentou fazer a questao. Minha resposta estava certa so tinha que da uma arrumada com as identidades trigonometricas.
Se alguem ficou interessado na questao,, a resposta é :
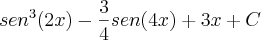
... e se nao conseguir chegar nessa forma utilize as identidades trigonometricas ou pede ajuda pra mim ou qlq um no forum

-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por LuizAquino » Dom Ago 21, 2011 21:14
por LuizAquino » Dom Ago 21, 2011 21:14
ewald escreveu:Consegui!!

Obrigado pra quem leu e tentou fazer a questao. Minha resposta estava certa so tinha que da uma arrumada com as identidades trigonometricas.
Esse problema é bem comum. Ainda mais em integrais trigonométricas. O estudante resolve a integral corretamente, mas quando confere o gabarito fica frustrado, pois está "diferente" do que ele obteve. Na verdade, o gabarito não está "diferente", mas apenas simplificado.
Fica então a lição: verifique se há alguma simplificação a fazer na resposta que você obteve quando for conferir o gabarito.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2838 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Seg Ago 22, 2011 00:44
- 1 Respostas
- 1424 Exibições
- Última mensagem por LuizAquino

Seg Ago 22, 2011 08:52
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Integral com função trigonometrica
por karenfreitas » Qui Jun 30, 2016 18:18
- 1 Respostas
- 3586 Exibições
- Última mensagem por adauto martins

Sáb Jul 09, 2016 18:18
Cálculo: Limites, Derivadas e Integrais
-
- [Dúvida]Função Trigonométrica Inversa em Integral.
por Jhonata » Qui Jun 07, 2012 18:06
- 2 Respostas
- 1935 Exibições
- Última mensagem por Jhonata

Qui Jun 07, 2012 20:40
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral trigonométrica
por -civil- » Sex Mar 30, 2012 03:05
- 1 Respostas
- 1592 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 18:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 [integral indef. de 48 vezes seno ao quadrado de x vezes coseno elevado a quarta potencia de x]
[integral indef. de 48 vezes seno ao quadrado de x vezes coseno elevado a quarta potencia de x]
 [integral indef. de 48 vezes seno ao quadrado de x vezes coseno elevado a quarta potencia de x]
[integral indef. de 48 vezes seno ao quadrado de x vezes coseno elevado a quarta potencia de x]
 Obrigado pra quem leu e tentou fazer a questao. Minha resposta estava certa so tinha que da uma arrumada com as identidades trigonometricas.
Obrigado pra quem leu e tentou fazer a questao. Minha resposta estava certa so tinha que da uma arrumada com as identidades trigonometricas. 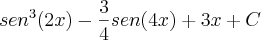


Obrigado pra quem leu e tentou fazer a questao. Minha resposta estava certa so tinha que da uma arrumada com as identidades trigonometricas.

