Note que a sua função é formada por três pedaços, cada um sendo uma porção de reta. Ora, uma função do tipo

(a e b constantes reais) é derivável em todos os pontos de seu domínio! (Se você quiser, facilmente pode demonstrar isso.)
Por exemplo, a função h(x) = x + 1 é derivável em todos os pontos de seu domínio (que seria o conjunto dos números reais). É claro que
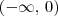
é um subconjunto do domínio de h, portanto ela é derivável nele. Em resumo, h é derivável para x < 0.
ObservaçãoPara provar que a sua função é diferenciável em todos os seus pontos, exceto em 0 e 1, você terá que provar que o limite

existe para três casos distintos:
(i) a < 0
(ii) 0 < a < 1
(iii) a > 1



 (a e b constantes reais) é derivável em todos os pontos de seu domínio! (Se você quiser, facilmente pode demonstrar isso.)
(a e b constantes reais) é derivável em todos os pontos de seu domínio! (Se você quiser, facilmente pode demonstrar isso.)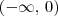 é um subconjunto do domínio de h, portanto ela é derivável nele. Em resumo, h é derivável para x < 0.
é um subconjunto do domínio de h, portanto ela é derivável nele. Em resumo, h é derivável para x < 0. existe para três casos distintos:
existe para três casos distintos: em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.