Maykids escreveu:eu até tentei usar o wolfram mais ele tem hora que modifica tudo, ln por log (...)
É apenas uma questão de notação. Ele usa "log" para representar o logaritmo natural (ou seja, na base "e"). Em resumo, nessa página (e em muitas outras de língua inglesa) temos que "log" representa "ln".
Maykids escreveu:(...) mais eu nao quero saber se realmente acertei, quero saber se estou fazendo algum passo errado , o que estou fazendo qe posso fazer de um modo mais facil, ou simplificado. esses sites so mostram se esta certo ou errado. (...)
Em particular, na página do Wolfram existe a opção "Show steps", que como o próprio nome já diz exibe o passo-a-passo da resolução. Esse passo-a-passo tipicamente já é o mais simplificado.
Por exemplo, digamos que você quer conferir a sua resolução para

.
Primeiro, insira na página o comando:
- Código: Selecionar todos
integrate[x^3 - 3*x^2 + 1, x]
Isso calculará a integral indefinida. Próximo ao resultado aparece o botão "Show steps". Clicando nele você pode acompanhar a resolução.
Em seguida, para verificar se o valor final da integral definida está correto, use o comando:
- Código: Selecionar todos
integrate[x^3 - 3*x^2 + 1, {x, 0, 2}]
 =
= 
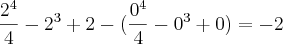
 =
= 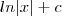
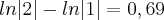
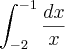 =
= 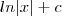

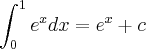
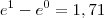
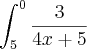
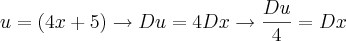






 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

