 por Rambox » Ter Jun 14, 2011 14:38
por Rambox » Ter Jun 14, 2011 14:38
Boa tarde tenho tenho estado a tentar resolver 2 exercícios de calculo de áreas usando integrais , mas acho que não estão correctamente resolvidos alguém
me poderia dar ajuda e verificar se o que eu estou a fazer está bem ?
1) Calcule a área limitada pelas linhas y =|X| e y = -x^2 + 2 ? Minha resolução :

Após determinar esses dois integrais multiplico o resultado por 2 para dar assim toda área e não só de metade ... mas não sei se está correcto
2) Determine o valor da área limitada pelas rectas X=2 ; X=0 ; Y=0 e pela curva x^3 - 3x^2 + 2x ?Minha resolução :
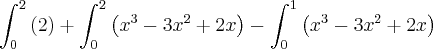
É possível o que fiz estar certo ? Se não estiver será que alguém me podia dar uma ajudinha a compreender estes 2 exercícios ?
Obrigado.
-
Rambox
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 14, 2011 14:04
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Ter Jun 14, 2011 14:45
por MarceloFantini » Ter Jun 14, 2011 14:45
Rambox, vocÊ está fazendo cálculo 1 ou 2? Segundo, você tentou desenhar a região de integração?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Rambox » Ter Jun 14, 2011 14:54
por Rambox » Ter Jun 14, 2011 14:54
Não entendi bem a sua primeira questão , mas sim na meti as funções na calculadora ela fez os gráficos e vi as regiões de integração , mas não tenho bem certeza se o que estou fazendo está correcto
-
Rambox
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 14, 2011 14:04
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo de áreas por integrais
 por Faby » Seg Set 19, 2011 10:50
por Faby » Seg Set 19, 2011 10:50
- 9 Respostas
- 6329 Exibições
- Última mensagem por Faby

Qui Set 22, 2011 00:41
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAIS UTILIZANDO AS IDENTIDADES TRIGONOMETRICAS
por Fabiano28 » Seg Mar 23, 2015 17:32
- 0 Respostas
- 1627 Exibições
- Última mensagem por Fabiano28

Seg Mar 23, 2015 17:32
Cálculo: Limites, Derivadas e Integrais
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8828 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais (áreas) [dúvida]
por citadp » Qua Jun 20, 2012 11:21
- 4 Respostas
- 3187 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 10:58
Cálculo: Limites, Derivadas e Integrais
-
- Interseção entre áreas (Integrais)
 por thejotta » Seg Abr 30, 2018 16:52
por thejotta » Seg Abr 30, 2018 16:52
- 3 Respostas
- 11211 Exibições
- Última mensagem por Gebe

Ter Mai 01, 2018 22:51
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 , avisa que eu resolvo.
, avisa que eu resolvo.

