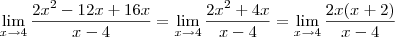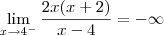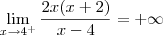por theSinister » Seg Mai 16, 2011 16:15
por theSinister » Seg Mai 16, 2011 16:15
percebi que existe limite para a função : f(x)=2x²-12x+16x / x-4 , quando x tende a 4 ,obviamente.
Porem ,acho que não preciso montar uma tabela para verificar isso ,basta fatorar a função: 2(x - (-2)) . (x-0) / x-4 , certo?
Porém não consegui progredir , tenho dificuldade em divisão de polinomios , como faço agora?
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Mai 16, 2011 19:53
por LuizAquino » Seg Mai 16, 2011 19:53
Note que "f(x)=2x²-12x+16x / x-4" é o mesmo que:
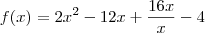
Por acaso a função não seria:
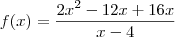
?
Nesse caso, você deveria ter escrito "f(x) = (2x² - 12x + 16x)/(x - 4)". Note que é fundamental usar adequadamente os delimitadores.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por theSinister » Seg Mai 16, 2011 20:10
por theSinister » Seg Mai 16, 2011 20:10
o correto é :
"f(x) = (2x² - 12x + 16x)/(x - 4)"
desculpe o erro.
mas como faço para fatorar? só consegui até aqui :
2(x - (-2)) . (x-0) / (x-4)
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Mai 16, 2011 20:21
por LuizAquino » Seg Mai 16, 2011 20:21
Nesse caso, temos que
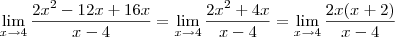
Esse limite não existe, pois os seus laterais são distintos:
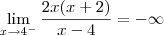
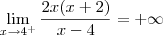 Sugestão
SugestãoEu acredito que o tópico abaixo possa lhe interessar:
Curso de Cálculo I no YouTubeviewtopic.php?f=137&t=4280
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por theSinister » Seg Mai 16, 2011 21:54
por theSinister » Seg Mai 16, 2011 21:54
obrigado pela indicação, mas gostaria de fatorar a função de forma a eliminar a divisão , e assim , substituir "x" por 4 , e saber o que acontece com a função quando o valor de x se aproxima de 4, seria possível isso?
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Mai 16, 2011 22:04
por LuizAquino » Seg Mai 16, 2011 22:04
Note que o polinômio 2x(x+2) não é divisível por (x-4). Isso significa que você não irá conseguir eliminar a fração que aparece no limite.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6644 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4790 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5119 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7259 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4436 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


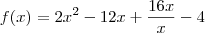
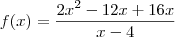 ?
?