 por aline_n » Qui Abr 28, 2011 10:03
por aline_n » Qui Abr 28, 2011 10:03
Calcule o coeficiente angular m da reta tangente ao grafico de cada funcao no ponto indicado.
b)

em (4, 1/2)
Solucao:

depois disso eu nao consigo resolver....
Me aajudem....
-
aline_n
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 28, 2011 09:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por LuizAquino » Qui Abr 28, 2011 10:16
por LuizAquino » Qui Abr 28, 2011 10:16
O limite correto é:
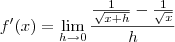
Isso é o mesmo que:
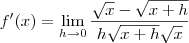
Para continuar a resolução basta multiplicar o numerador e o denominador por
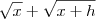
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas]Eq da reta tangente e normal
por may » Ter Mai 14, 2013 04:41
- 1 Respostas
- 2065 Exibições
- Última mensagem por adauto martins

Qua Out 15, 2014 21:02
Cálculo: Limites, Derivadas e Integrais
-
- [Equação da reta Tangente] derivadas
por lucasdemirand » Qua Ago 07, 2013 00:28
- 1 Respostas
- 2100 Exibições
- Última mensagem por young_jedi

Qua Ago 07, 2013 20:12
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas inclinacao da reta tangente
por Gabrielmelocampos20 » Qui Nov 12, 2015 20:46
- 1 Respostas
- 2448 Exibições
- Última mensagem por Cleyson007

Sex Nov 13, 2015 08:35
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Encontrar a equação da reta tangente
por MrJuniorFerr » Qua Out 17, 2012 12:01
- 1 Respostas
- 2279 Exibições
- Última mensagem por MarceloFantini

Qua Out 17, 2012 12:21
Cálculo: Limites, Derivadas e Integrais
-
- A reta tangente ao gráfico da função (derivadas)
por Ana Maria da Silva » Dom Jun 09, 2013 21:43
- 2 Respostas
- 2068 Exibições
- Última mensagem por Ana Maria da Silva

Qua Jun 12, 2013 20:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 em (4, 1/2)
em (4, 1/2)

 em (4, 1/2)
em (4, 1/2)

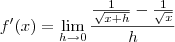
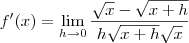
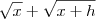 .
.

 .
.
 :
: