 por johnny » Ter Abr 12, 2011 00:46
por johnny » Ter Abr 12, 2011 00:46
Pretende-se estender um cabo de uma usina de força à margem de um rio de
900 m de largura até uma fabrica situada do outro lado do rio, 3000 m rio abaixo. O
custo para estender um cabo pelo rio é de R$ 5,00 o metro, enquanto que para
estende-lo por terra custa R$ 4,00 o metro. Qual é o percurso mais econômico
para o cabo? tentei resouver assim
C t= C rio +C terra
C t= R$ 5,00 . R + R$ 4.00 .T
C t= 5.00.\sqrt[]{{900}^{2}+{x}^{2}}. 4.00.(3000-x)
C t= 5.00.({900}^{2}+{x}^{2})^{1/2} + 4.00 . (3000-x)
e agora derivo. so consegui chegar ate aqui, fiz alguns cauculo, mas n deu serto.
Editado pela última vez por
johnny em Ter Abr 12, 2011 01:11, em um total de 4 vezes.
-
johnny
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Out 22, 2010 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari de produção
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 00:52
por FilipeCaceres » Ter Abr 12, 2011 00:52
Poderia arrumar a tua equação, não dá para ver nada.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por johnny » Ter Abr 12, 2011 00:54
por johnny » Ter Abr 12, 2011 00:54
n to conceguindo postar meu rasocinio.
-
johnny
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Out 22, 2010 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari de produção
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 00:57
por FilipeCaceres » Ter Abr 12, 2011 00:57
Faz o seguinte, apenas tire os tex /tex para que possamos ver o que vc esta errando.
Abraço
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Ter Abr 12, 2011 00:58
por FilipeCaceres » Ter Abr 12, 2011 00:58
Eu acho que eu você colocou [/tex] a mais e por isso deve estar dando erro.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por johnny » Ter Abr 12, 2011 01:12
por johnny » Ter Abr 12, 2011 01:12
deu para ver agora,
-
johnny
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Out 22, 2010 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari de produção
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 01:25
por FilipeCaceres » Ter Abr 12, 2011 01:25
O objetivo é minimizar o custo de instalação do cabo. Logo, precisamos construir a função custo.
Arrumando a tua equação

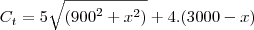
Observe que x e 3.000 – x não podem ser negativos, a região de interesse (domínio do problema) é o
intervalo [0, 3.000], onde devemos encontrar o mínimo absoluto de C.
Agora é só derivar C e igualar a zero para encontrar seus pontos críticos.
Abraço qualquer coisa poste a sua dúvida.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por johnny » Ter Abr 12, 2011 01:37
por johnny » Ter Abr 12, 2011 01:37
para resolver a derivada troco a raiz por e elevo a 1/2,
-
johnny
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Out 22, 2010 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari de produção
- Andamento: cursando
 por johnny » Ter Abr 12, 2011 01:44
por johnny » Ter Abr 12, 2011 01:44
n com sigo resolver a derivada.
pode me ajudar
-
johnny
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Out 22, 2010 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari de produção
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 01:45
por FilipeCaceres » Ter Abr 12, 2011 01:45
Esta vai ser a derivada,
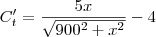
Tente chegar nela, se tiver dúvida poste novamente.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por johnny » Ter Abr 12, 2011 02:00
por johnny » Ter Abr 12, 2011 02:00
n consegui chegar ate essa derivada, mas continuei a resouver. ficol assim.
![\sqrt[]{{900}^{2}+{x}^{2}}=5x-4 \sqrt[]{{900}^{2}+{x}^{2}}=5x-4](/latexrender/pictures/ee4131b4579039d1f126eb916f7ab22a.png)
corta-se a raiz
900+x=5x-4
900+4=5x-x
4x=904
x=904/4
x=226
esta correto
-
johnny
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Out 22, 2010 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari de produção
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 02:11
por FilipeCaceres » Ter Abr 12, 2011 02:11
Fazendo
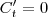
temos,
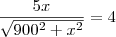

Elevando ao quadrado, temos


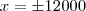
Como x deve ser positivo e

![\epsilon [0, 3.000] \epsilon [0, 3.000]](/latexrender/pictures/7aaabefd9e92f142b5bab247b8efcfca.png)
, segue que é o único ponto crítico de C, no domínio
de interesse.
Para saber se é mínimo absoluto precisamos comparar o valor de C neste ponto com
os valores nos extremos do domínio. Assim, temos:

,
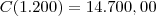
e
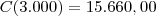
.
Portanto, que o custo mínimo para a instalação do cabo será de R$ 14.700,00 e, para obtê-lo,
o cabo deverá percorrer 1.800 metros por terra, a partir da fábrica, e depois ir por água até a usina.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por johnny » Ter Abr 12, 2011 02:20
por johnny » Ter Abr 12, 2011 02:20
se n for pedir muito gostaria de entender como vc chegou aquela derivada, pode me ensinar apartir da equação
-
johnny
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Out 22, 2010 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari de produção
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 10:09
por FilipeCaceres » Ter Abr 12, 2011 10:09
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por johnny » Qua Abr 13, 2011 00:21
por johnny » Qua Abr 13, 2011 00:21
obrigado pela sua esplicação me ajudou bastante. brigadão
-
johnny
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Out 22, 2010 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari de produção
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









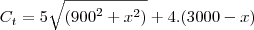



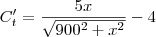

![\sqrt[]{{900}^{2}+{x}^{2}}=5x-4 \sqrt[]{{900}^{2}+{x}^{2}}=5x-4](/latexrender/pictures/ee4131b4579039d1f126eb916f7ab22a.png)

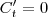 temos,
temos,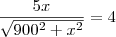



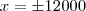

![\epsilon [0, 3.000] \epsilon [0, 3.000]](/latexrender/pictures/7aaabefd9e92f142b5bab247b8efcfca.png) , segue que é o único ponto crítico de C, no domínio
, segue que é o único ponto crítico de C, no domínio ,
, 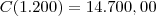 e
e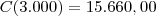 .
.


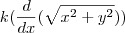
 , então
, então 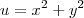 logo,
logo,
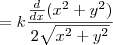






![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.