Bom, estou começando a disciplina de Cálculo II, e estou tendo dificuldade nesse início com as integrais.
Bom, vamos a um exercício bem simples até que eu vá aprendendo os "macetes":
Prove que
A apostila que uso descreve o seguinte:
"Sabendo que F(x) é uma primitiva de f(x), temos que
". Primeiramente, explique-me essa notação. Depois explique o procedimento de resolução passo-a-passo.Aguardo retorno.
Agradeço a atenção.
que seria: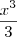
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)