 por vmouc » Sex Mar 11, 2011 23:51
por vmouc » Sex Mar 11, 2011 23:51
Calcule os limites se existir:
Pessoal, gostaria de confirmar se minhas respostas estão corretas, por favor, me ajudem!

pela forma de substituição daria

pela forma de fatoração ficaria
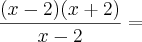
? x=2 e
e)

f)
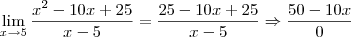
ou seja, o denominador =0.O que eu faço aqui, please? rsrs
As outras estão corretas?
Muito obrigado pela ajuda!
Editado pela última vez por
vmouc em Sáb Mar 12, 2011 00:13, em um total de 2 vezes.
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por LuizAquino » Sáb Mar 12, 2011 00:04
por LuizAquino » Sáb Mar 12, 2011 00:04
Os exercícios a), b) e e) estão ok.
c) Dica:
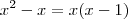
d) Dica:

f) Dica:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vmouc » Sáb Mar 12, 2011 00:06
por vmouc » Sáb Mar 12, 2011 00:06
Eu não entendi como ficará o resultado destes limites. Não é um valor exato?
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por LuizAquino » Sáb Mar 12, 2011 00:09
por LuizAquino » Sáb Mar 12, 2011 00:09
Após usar as dicas que eu indiquei você poderá fazer simplificações que removerão a indeterminação de cada um dos limites.
Uma vez que as indeterminações forem removidas, você pode resolver os limites usando a mesma ideia usada nos outros limites que você resolveu.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vmouc » Sáb Mar 12, 2011 00:37
por vmouc » Sáb Mar 12, 2011 00:37
Eu só não tiver certeza na f).
Dá uma olhadinha nas outras por favor:
c)
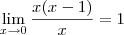
d)
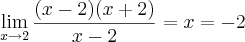
f)
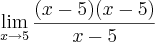
aqui zera.

seria isto?
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por vmouc » Sáb Mar 12, 2011 11:05
por vmouc » Sáb Mar 12, 2011 11:05
Sempre tem que usar o método de substituição nesses casos?
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por LuizAquino » Sáb Mar 12, 2011 11:21
por LuizAquino » Sáb Mar 12, 2011 11:21
Presumo que você esteja no início do curso de Cálculo.
Desse modo, o que usamos para resolver esses limites foram as Propriedades Operatórias dos limites e o conhecimento dos limites:

e

, sendo
c uma constante.
Por exemplo, o limite
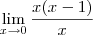
é o mesmo que
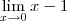
.
Uma das Propriedades Operatórias dos limites diz que "o limite da subtração é a subtração dos limites". Portanto, temos que
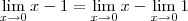
.
Usando os dois limites conhecidos acima, temos que
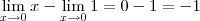
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vmouc » Sáb Mar 12, 2011 21:51
por vmouc » Sáb Mar 12, 2011 21:51
Pessoal,
continuando esta lista, não faço idéia como resolvo isso:
![\lim_{x\rightarrow10}\left[1n(10-x) \right] \lim_{x\rightarrow10}\left[1n(10-x) \right]](/latexrender/pictures/45e72c2c793aa426ccced41f835107e8.png)
Help, please! Estou estudando as outras e postarei a continuação desse exercício para que me ajudem na correção.
Muito Obrigado!!!
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por LuizAquino » Dom Mar 13, 2011 01:34
por LuizAquino » Dom Mar 13, 2011 01:34
ObservaçãoEsse limite só está bem definido pela direita. Portanto, o exercício deve ser:
 Sugestão
SugestãoObserve o gráfico da função

e tente responder o exercício.

- grafico-logaritmo-natural.png (7.41 KiB) Exibido 5362 vezes
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites exercícios
por hugohggomes » Ter Jun 14, 2016 17:34
- 0 Respostas
- 2432 Exibições
- Última mensagem por hugohggomes

Ter Jun 14, 2016 17:34
Cálculo: Limites, Derivadas e Integrais
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 3294 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4750 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4774 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


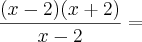 ? x=2 e
? x=2 e 
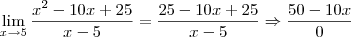 ou seja, o denominador =0.O que eu faço aqui, please? rsrs
ou seja, o denominador =0.O que eu faço aqui, please? rsrs

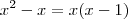



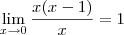
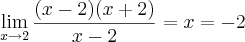
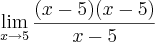 aqui zera.
aqui zera. seria isto?
seria isto?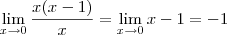
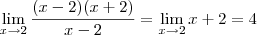

 e
e  , sendo
, sendo 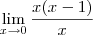 é o mesmo que
é o mesmo que 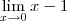 .
.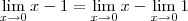 .
.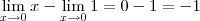 .
.![\lim_{x\rightarrow10}\left[1n(10-x) \right] \lim_{x\rightarrow10}\left[1n(10-x) \right]](/latexrender/pictures/45e72c2c793aa426ccced41f835107e8.png)

 e tente responder o exercício.
e tente responder o exercício.