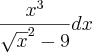
Se alguém puder me ajudar ficarei grata.


Manoella escreveu:Ajude me a decifrar essa integral:
Se alguém puder me ajudar ficarei grata.
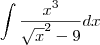
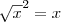 . Sendo assim, essa integral é a mesma que:
. Sendo assim, essa integral é a mesma que: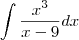
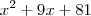 e o resto será 729, ou seja,
e o resto será 729, ou seja, 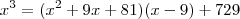 . Desse modo, temos que:
. Desse modo, temos que: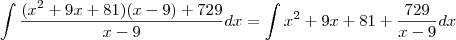
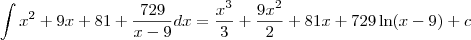 , com c uma constante.
, com c uma constante.
![\frac{x^3}{\sqrt[]{x^2-9}}dx \frac{x^3}{\sqrt[]{x^2-9}}dx](/latexrender/pictures/f6d1b2f92b7c91e6cc34322189876a98.png)

Manoella escreveu:Realmente cometi um serio erro ao digitar, na realidade a integral que quero é essa. Desculpas pela falha;
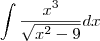
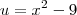 , então
, então  . Desse modo, obtemos:
. Desse modo, obtemos: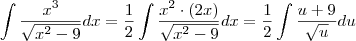
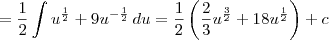
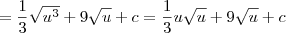 , onde c é uma constante.
, onde c é uma constante.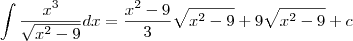
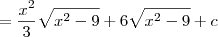

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes

 .
.
 :
: