
![y=ln(\frac{\sqrt[]{sen\theta*cos\theta}}{1+2ln\theta}) y=ln(\frac{\sqrt[]{sen\theta*cos\theta}}{1+2ln\theta})](/latexrender/pictures/6ad26e558d8f45918ad17fc407855d42.png)
Resp.: Micrsoft Math
![\frac{cos(\theta)^2-sen(\theta)^2}{(4ln(\theta)+2)*\sqrt[]{sen\theta*cos\theta}}-\frac{2.\sqrt[]{sen\theta*con\theta}}{\theta(2ln\theta+1)^2} \frac{cos(\theta)^2-sen(\theta)^2}{(4ln(\theta)+2)*\sqrt[]{sen\theta*cos\theta}}-\frac{2.\sqrt[]{sen\theta*con\theta}}{\theta(2ln\theta+1)^2}](/latexrender/pictures/4bc0bf7ceb887d868fa1a85b660a1196.png)
Resp.: HP 50
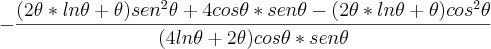
Desde já agradeço.



 para realizar a segunda derivada e fazer semelhante para realizar a primeira derivada chamando de
para realizar a segunda derivada e fazer semelhante para realizar a primeira derivada chamando de  .
.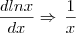
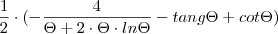

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)