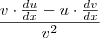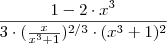por ARCS » Ter Jan 18, 2011 18:22
por ARCS » Ter Jan 18, 2011 18:22
Estou com dificuldade na resolução dessa derivada.
Dada
![f (x) =\sqrt[3]{\frac{x}{x^3+1}} f (x) =\sqrt[3]{\frac{x}{x^3+1}}](/latexrender/pictures/caf5f00aa2714bc63966e8f65ca25765.png)
Calcule a f´(x)
Incialmente eu transformei a fração em produto porque é bem mais prático usar a regra do produto ao invés da do quociente.
Logo,
![f (x) =\sqrt[3]{\frac{x}{x^3+1}} = {x}^{1/3}{(x^3+1)}^{-1/3} f (x) =\sqrt[3]{\frac{x}{x^3+1}} = {x}^{1/3}{(x^3+1)}^{-1/3}](/latexrender/pictures/73f3b61c728598539edefde0aff5a617.png)
Combinado a regra do produto com a regra da cadeia, obtemos:
Aplicando a regra do produto, temos:

Aplicando a regra da cadeia, temos:
![f'(x) = {x}^{1/3}[\frac{-1}{3}{(x^3+1)}^{-4/3}(3x^2)] + [ \frac{1}{3}{x}^{-2/3}]{(x^3+1)}^{-1/3} f'(x) = {x}^{1/3}[\frac{-1}{3}{(x^3+1)}^{-4/3}(3x^2)] + [ \frac{1}{3}{x}^{-2/3}]{(x^3+1)}^{-1/3}](/latexrender/pictures/6f26960fc090bf7c8da9379408b8d4b4.png)
Meu professor disse que até aí esta correto, basta agora colocar algum termo em evidência para obter

Mas não estou conseguindo.
Favor explicar detalhadamente
Editado pela última vez por
ARCS em Qua Jan 19, 2011 15:56, em um total de 1 vez.
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Renato_RJ » Ter Jan 18, 2011 20:11
por Renato_RJ » Ter Jan 18, 2011 20:11
Eu fiz uma abordagem diferente da tua, veja:
![f(x) = \sqrt[3]{\frac{x}{x^3+1}} f(x) = \sqrt[3]{\frac{x}{x^3+1}}](/latexrender/pictures/403c0ca76f7c11ad98441e3cdf0ea7ce.png)
Fazendo

temos:
![\frac{d u^{2/3}}{du} \Rightarrow \, \frac{1}{3 \cdot \sqrt [3] {u^2}} \cdot u` \frac{d u^{2/3}}{du} \Rightarrow \, \frac{1}{3 \cdot \sqrt [3] {u^2}} \cdot u`](/latexrender/pictures/c34568fbf96ee459c54b1ca515dfbb85.png)
Fazendo a derivada de u, teremos:

Agora usarei a regra do quociente chamando de

e
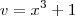
teremos:
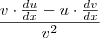
Logo:

Com uma básica manipulação teremos:
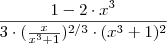
Resolvendo o denominador, teremos:

O que nos leva a resposta:

Eu acho que está certo, mas como sou humano, posso ter errado em algum lugar, se alguém puder confirmar essas contas ficarei imensamente grato.
Abraços,
Renato
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por ARCS » Qua Jan 19, 2011 18:20
por ARCS » Qua Jan 19, 2011 18:20
Valew pela resposta, mais ainda não entendi.
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com questões de derivadas! Urgente!
por arthurvct » Qua Jun 05, 2013 15:59
- 1 Respostas
- 1081 Exibições
- Última mensagem por ericaguedes_

Sáb Jun 08, 2013 00:07
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2263 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7481 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4957 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2969 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f (x) =\sqrt[3]{\frac{x}{x^3+1}} f (x) =\sqrt[3]{\frac{x}{x^3+1}}](/latexrender/pictures/caf5f00aa2714bc63966e8f65ca25765.png)
![f (x) =\sqrt[3]{\frac{x}{x^3+1}} = {x}^{1/3}{(x^3+1)}^{-1/3} f (x) =\sqrt[3]{\frac{x}{x^3+1}} = {x}^{1/3}{(x^3+1)}^{-1/3}](/latexrender/pictures/73f3b61c728598539edefde0aff5a617.png)

![f'(x) = {x}^{1/3}[\frac{-1}{3}{(x^3+1)}^{-4/3}(3x^2)] + [ \frac{1}{3}{x}^{-2/3}]{(x^3+1)}^{-1/3} f'(x) = {x}^{1/3}[\frac{-1}{3}{(x^3+1)}^{-4/3}(3x^2)] + [ \frac{1}{3}{x}^{-2/3}]{(x^3+1)}^{-1/3}](/latexrender/pictures/6f26960fc090bf7c8da9379408b8d4b4.png)



![f(x) = \sqrt[3]{\frac{x}{x^3+1}} f(x) = \sqrt[3]{\frac{x}{x^3+1}}](/latexrender/pictures/403c0ca76f7c11ad98441e3cdf0ea7ce.png)
 temos:
temos:![\frac{d u^{2/3}}{du} \Rightarrow \, \frac{1}{3 \cdot \sqrt [3] {u^2}} \cdot u` \frac{d u^{2/3}}{du} \Rightarrow \, \frac{1}{3 \cdot \sqrt [3] {u^2}} \cdot u`](/latexrender/pictures/c34568fbf96ee459c54b1ca515dfbb85.png)

 e
e 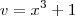 teremos:
teremos: