Olá.
Sobre as aplicações em administração, não sou habilitado para dizer, mas vale comentar que o estudo da matemática em si não se restringe às aplicações. De qualquer forma, posso citar curvas de demanda como exemplo, onde se faz uso de integrais. E ao falar de cálculo: limites e assíntotas são exemplos de pré-requisitos! Mesmo que por ora você não encontre aplicações relacionadas às assíntotas, certamente encontrará para derivadas e integrais.
Para seu estudo de assíntotas, pense inicialmene em uma hipérbole, por exemplo a função

.
Há uma assíntota vertical e outra horizontal.
Quanto x tende a zero, o valores de y ficam arbitrariamente grandes (em módulo).
A reta

é a assíntota vertical que nunca e tocada pela hipérbole.
Por outro lado, quanto tornamos x arbitrariamente grande (em módulo), notamos que o valor da função tende a zero, os valores de y ficam arbitrariamente pequenos (em módulo).
A reta

é a assíntota horizontal que também nunca é tocada pela hipérbole.
Considero que este seja o exemplo mais didático para extrair este entendimento. Pense com o gráfico.
Para descobrir as assíntotas, você precisará utilizar limites.
Em geral, a assíntota vertical é determinada por alguma restrição no denominador por ser zero.
A assíntota horizontal obtemos analisando o limite da função quando

.
Veja, no segundo exercício que você enviou, vimos que o limite da função quando

é zero (o limite é 0).
Ou seja, a reta

é a assíntota horizontal.
Sugiro ler a teoria no livro do Stewart sobre limites no infinito, assíntotas horizontais e verticais.
Se necessário, comente após suas tentativas.
Espero ter ajudado e bons estudos!
 ______________________
______________________ + 6x³ +9
+ 6x³ +9

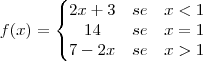
 , os limites laterais devem ser iguais.
, os limites laterais devem ser iguais.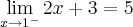
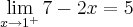
 , tanto é que
, tanto é que 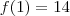 .
.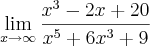
 , temos:
, temos:


 .
. é a assíntota vertical que nunca e tocada pela hipérbole.
é a assíntota vertical que nunca e tocada pela hipérbole. é a assíntota horizontal que também nunca é tocada pela hipérbole.
é a assíntota horizontal que também nunca é tocada pela hipérbole. .
.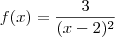
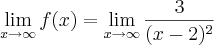

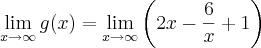
 , o que indica não existir assíntota horizontal (pense no gráfico).
, o que indica não existir assíntota horizontal (pense no gráfico).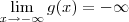 .
.