 por rafacosme » Qui Jun 17, 2010 12:29
por rafacosme » Qui Jun 17, 2010 12:29
Olha eu mais uma vez rs.
Então, agora a dúdiva é uma questão sobre limites..
Sei que devo estar enchendo um pouco com tanta pergunta, mas é porque vou ter prova hoje hehe.
Obrigado mais uma vez


-
rafacosme
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Jun 16, 2010 15:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação ( CComp_)
- Andamento: cursando
 por MarceloFantini » Qui Jun 17, 2010 12:50
por MarceloFantini » Qui Jun 17, 2010 12:50
Se o limite existe, isso significa que quando
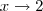
tanto o numerador como o denominador tendem a zero. Tirando a constante

do limite, fica:
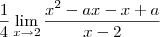
. Fatorando o numerador:
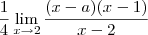
O único jeito de essa expressão ter um limite é se a = 2, caso contrário ele não existe.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rafacosme » Qui Jun 17, 2010 13:14
por rafacosme » Qui Jun 17, 2010 13:14
Hmm, de onde saiu o x-2 do denominador?
o unico valor para haver limité é 2 porque o resultado no final tem que ser igual a zero?
-
rafacosme
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Jun 16, 2010 15:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação ( CComp_)
- Andamento: cursando
 por MarceloFantini » Sex Jun 18, 2010 08:30
por MarceloFantini » Sex Jun 18, 2010 08:30
Eu posso colocar o 4 em evidência no denominador no limite original. Só que esse 4 em evidência é a mesma coisa que

no limite, pois é uma constante.
Não entendi a sua segunda pergunta. Não tem nada igual a zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rafacosme » Sex Jun 18, 2010 11:54
por rafacosme » Sex Jun 18, 2010 11:54
É, não consegui expressar o que queria perguntar mas já entendi e já fiz a prova!
Obrigado Fantini.
Tirei 10 na prova =]
-
rafacosme
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Jun 16, 2010 15:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação ( CComp_)
- Andamento: cursando
 por MarceloFantini » Sex Jun 18, 2010 18:21
por MarceloFantini » Sex Jun 18, 2010 18:21
Parabéns!
E refletindo mais um pouco, acho que entendi a sua pergunta. Você queria perguntar porque que tanto o numerador como o denominador tem que tender a zero, não era isso? A resposta é porque se não for assim, a função foge do controle, e pode ser que não exista limite como um número real.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rafacosme » Sex Jun 18, 2010 21:11
por rafacosme » Sex Jun 18, 2010 21:11
Obrigado

Foi isso mesmo hehe!
Acertou mais uma vez

E mais uma vez obrigado pela ajuda!
Semestre que vem agora vou ter matemática básica que é Algebra Linear e Geometria Analítica, sendo que não gosto nenhum pouco de Algebra..
Esse semestre foi calculo 1 junto com calculo 2..
-
rafacosme
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Jun 16, 2010 15:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação ( CComp_)
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- É preciso saber limite para derivada e integral?
por mineirodointerior » Qui Out 15, 2015 00:34
- 2 Respostas
- 6859 Exibições
- Última mensagem por Cleyson007

Sáb Out 17, 2015 00:04
Cálculo: Limites, Derivadas e Integrais
-
- só queria saber, o que fazer com -x(0,9941644) para chegar e
por Bruno1800 » Ter Mai 17, 2016 09:53
- 1 Respostas
- 1747 Exibições
- Última mensagem por nakagumahissao

Qui Mai 19, 2016 06:39
Equações
-
- Preciso saber a fórmula para resolver esse exercício
por Dankaerte » Qui Ago 27, 2009 14:19
- 1 Respostas
- 6963 Exibições
- Última mensagem por Molina

Qui Ago 27, 2009 14:58
Geometria Plana
-
- Quando saber que não existe um limite ?
por OtavioBonassi » Qua Jan 05, 2011 15:14
- 6 Respostas
- 52579 Exibições
- Última mensagem por OtavioBonassi

Qua Jan 05, 2011 19:48
Cálculo: Limites, Derivadas e Integrais
-
- Gostaria de saber como calcular o seguinte limite
por felipe_08 » Qui Abr 23, 2015 17:36
- 2 Respostas
- 2575 Exibições
- Última mensagem por felipe_08

Qui Abr 23, 2015 22:51
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






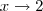 tanto o numerador como o denominador tendem a zero. Tirando a constante
tanto o numerador como o denominador tendem a zero. Tirando a constante  do limite, fica:
do limite, fica: 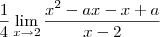 . Fatorando o numerador:
. Fatorando o numerador: 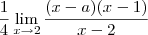



 no limite, pois é uma constante.
no limite, pois é uma constante.







 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.