 por SOPMod » Ter Jun 15, 2010 01:11
por SOPMod » Ter Jun 15, 2010 01:11
Olá! Este é meu primeiro post nesse fórum.
Bem, meus problemas com integrais, em parte, vêm das belezuras com raiz quadrada. Eu simplesmente não consigo integrar uma expressão com raiz quadrada (exceto quando há um termo que multiplica ela, daí faço substituição). Já vi recomendarem o uso de tabelas de integrais, mas como eu decoro tudo aquilo? E pior, recomendaram usar as trigonométricas, mas como eu escolho a função de acordo com o exercício?
Bem, mando 2 exercícios exemplo:
![\int_{}^{}\sqrt[2]{3-{4x}^{2}} \int_{}^{}\sqrt[2]{3-{4x}^{2}}](/latexrender/pictures/e9d4299586a1c47d6abfb7c9e30aab81.png)
o outro:
![\int_{}^{}\sqrt[2]{9-(\left{x-1}\right)^{2}} \int_{}^{}\sqrt[2]{9-(\left{x-1}\right)^{2}}](/latexrender/pictures/f5e766f1737d9e099e1e06a46c696132.png)
eu tentei resolver usando substituição e integração por partes, mas não dá certo. Olhei no wolframalpha o resultado e como ele chegou lá, mas não entendi o critério usado para substituir os valores de x.
-
SOPMod
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jun 15, 2010 00:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciência da Computação
- Andamento: cursando
 por MatheusAgostin » Dom Jun 20, 2010 18:58
por MatheusAgostin » Dom Jun 20, 2010 18:58
-
MatheusAgostin
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 20, 2010 12:19
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7302 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Raiz quadrada
por j1a4l0 » Qui Abr 22, 2010 18:05
- 5 Respostas
- 5802 Exibições
- Última mensagem por Neperiano

Sex Abr 23, 2010 09:35
Funções
-
- raiz quadrada
por jose henrique » Seg Ago 16, 2010 16:54
- 1 Respostas
- 2262 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:03
Álgebra Elementar
-
- [Raiz quadrada de 13] Na mão
por Mickdark » Dom Abr 08, 2012 20:00
- 4 Respostas
- 17458 Exibições
- Última mensagem por Mickdark

Qui Abr 12, 2012 09:56
Álgebra Elementar
-
- Raiz quadrada
por anneliesero » Qua Dez 12, 2012 19:26
- 1 Respostas
- 2006 Exibições
- Última mensagem por replay

Qua Dez 19, 2012 16:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\sqrt[2]{3-{4x}^{2}} \int_{}^{}\sqrt[2]{3-{4x}^{2}}](/latexrender/pictures/e9d4299586a1c47d6abfb7c9e30aab81.png)
![\int_{}^{}\sqrt[2]{9-(\left{x-1}\right)^{2}} \int_{}^{}\sqrt[2]{9-(\left{x-1}\right)^{2}}](/latexrender/pictures/f5e766f1737d9e099e1e06a46c696132.png)


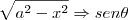

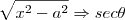


![\int_{}^{}\sqrt[]{3 - 4x^2)}dx \int_{}^{}\sqrt[]{3 - 4x^2)}dx](/latexrender/pictures/5e49c6eb7c50abcb020ce7f9a8cbe27c.png)
![\int_{}^{}\sqrt[]{4(\frac{3}{4} - x^2)}dx \int_{}^{}\sqrt[]{4(\frac{3}{4} - x^2)}dx](/latexrender/pictures/c7ce1b81760df0413a4e252528af8d44.png)
![2\int_{}^{}\sqrt[]{(\frac{3}{4} - x^2)}dx 2\int_{}^{}\sqrt[]{(\frac{3}{4} - x^2)}dx](/latexrender/pictures/3d10c71f34b9b15835a09fa7c24f8978.png)
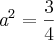
![\emph{a} = \frac{\sqrt[]{3}}{2} \emph{a} = \frac{\sqrt[]{3}}{2}](/latexrender/pictures/fa3ee269c17ad9d5957f287505d2824d.png)

![x = \frac{\sqrt[]{3}}{2}sen\theta x = \frac{\sqrt[]{3}}{2}sen\theta](/latexrender/pictures/f72abcf2f6ab0940fb78b2ba9b75eca7.png)
![dx = \frac{\sqrt[]{3}}{2}cos\theta d\theta dx = \frac{\sqrt[]{3}}{2}cos\theta d\theta](/latexrender/pictures/a86ef9b1ebba09c6a8afe550a3a27b47.png)
![2\int_{}^{}\frac{\sqrt[]{3}}{2}\sqrt[]{(1 - sen^2\theta)}.\frac{\sqrt[]{3}}{2}cos\theta d\theta 2\int_{}^{}\frac{\sqrt[]{3}}{2}\sqrt[]{(1 - sen^2\theta)}.\frac{\sqrt[]{3}}{2}cos\theta d\theta](/latexrender/pictures/c77ca56d77e47be02b6501baf9d821ec.png)
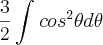
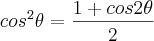
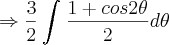
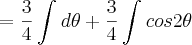
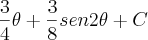
![\theta = arcsen\frac{2x}{\sqrt[]{3}} = arcsen \frac{2\sqrt[]{3}x}{3} \theta = arcsen\frac{2x}{\sqrt[]{3}} = arcsen \frac{2\sqrt[]{3}x}{3}](/latexrender/pictures/07a11ee6fe5df60b7eb47c48ec00004e.png)
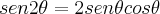
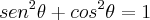
![cos\theta = \sqrt[]{1 - sen^2\theta} cos\theta = \sqrt[]{1 - sen^2\theta}](/latexrender/pictures/f274159d7bf3cfab780f072588905b7e.png)
![sen\theta = \frac{2\sqrt[]{3}x}{3} sen\theta = \frac{2\sqrt[]{3}x}{3}](/latexrender/pictures/79f4181d0871082c26b7f4757f376860.png)
![sen2\theta = \frac{4}{3}x \sqrt[]{3 - 4x^2} sen2\theta = \frac{4}{3}x \sqrt[]{3 - 4x^2}](/latexrender/pictures/86d6cdc9acedcf864612b917967bad2c.png)
![\int_{}^{}\sqrt[]{3 - 4x^2)}dx = \frac{3}{4}arcsen \frac{2\sqrt[]{3}x}{3} + \frac{1}{2}x \sqrt[]{3 - 4x^2} + C \int_{}^{}\sqrt[]{3 - 4x^2)}dx = \frac{3}{4}arcsen \frac{2\sqrt[]{3}x}{3} + \frac{1}{2}x \sqrt[]{3 - 4x^2} + C](/latexrender/pictures/318ee57bf4f4283c6e8c078c7d010597.png)