aí vai:
4- Determinar as dimensões de um cilindro, inscrito em uma esfera de raio R, cuja área da superfície externa total é a máxima possível.
Resposta: r = raio da base =
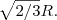h= altura do cilindro =
6- Quer-se construir um tanque de aço para armazenar gás propano, com a forma de um cilindro circular reto, com um hemisfério (semi-esfera) em cada extremidade. Se a capacidade desejada para o tanque é 100 decímetros cúbicos (litros), quais as dimensões que exigem a menor quantidade de aço? (despreze a espessura das paredes do tanque).
Resposta: O tanque deve ser esférico, de raio
![\sqrt[3]{75/\Pi}](/latexrender/pictures/f387079ac22be5a4524c7a94af9becf5.png "\sqrt[3]{75/\Pi}")
8-Um veterinário tem 100m de tela de arame. Com isto deseja construir seis canis, primeiro cercando uma gerião retangular e depois subdividindo essa região em seis retângulos menores, através de cinco cercas divisórias internas, paralelas a um dos lados. Que dimensões externas, dessa região retangular, maximizam sua área total, se o veterinário dasta os 100m de tela nessa construção?
Resposta: 25m por 50/7
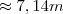
o 8 eu nem consegui começar, o 4 eu acho a relação
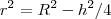e substituo na fórmula da área do cilindro: A = 
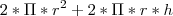, derivo, tentei de tudo mas não dá certo. O mesmo vai pro exercício 6.agradeço desde já,
Cassio
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.